Blocage dans factorisation [Résolu]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ketur
- Messages: 9
- Enregistré le: 30 Sep 2012, 19:59
-
 par Ketur » 30 Sep 2012, 20:05
par Ketur » 30 Sep 2012, 20:05
Bonsoir,
J'ai un DM pour demain et dans mon DM, on me dit de factoriser
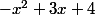
.
Voilà ce que j'ai commencé :
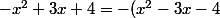)
(:ptdr: c'est un peu cour mais bon). Veuillez m'aider s'il vous plaît,
je suis dessus depuis 1 heure :mur:.
Merci d'avance.
-
low geek
- Membre Relatif
- Messages: 318
- Enregistré le: 02 Jan 2011, 19:09
-
 par low geek » 30 Sep 2012, 20:29
par low geek » 30 Sep 2012, 20:29
si tu trouve les deux racines du trinome tu peux factoriser par (x-x1) et par x-x2 ;)
-
Ketur
- Messages: 9
- Enregistré le: 30 Sep 2012, 19:59
-
 par Ketur » 30 Sep 2012, 20:36
par Ketur » 30 Sep 2012, 20:36
J'ai continué avec :
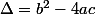
alors

donc

.
Comme
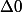
alors la factorisation est impossible.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 30 Sep 2012, 20:38
par ThekamikazeFou » 30 Sep 2012, 20:38
Ketur a écrit:J'ai continué avec :
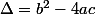
alors

donc

.
Comme
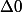
alors la factorisation est impossible.
tu as fais une erreur;
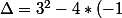*4 = 9+16 = 25)
-
Ketur
- Messages: 9
- Enregistré le: 30 Sep 2012, 19:59
-
 par Ketur » 30 Sep 2012, 20:45
par Ketur » 30 Sep 2012, 20:45
ThekamikazeFou a écrit:tu as fais une erreur;
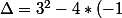*4 = 9+16 = 25)
Merci ! Donc maintenant je fais
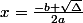
ou

donc
})
ou
})
?
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 30 Sep 2012, 20:47
par ThekamikazeFou » 30 Sep 2012, 20:47
Ketur a écrit:Merci ! Donc maintenant je fais
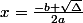
ou

donc
})
ou
})
?
exacte et

-
Ketur
- Messages: 9
- Enregistré le: 30 Sep 2012, 19:59
-
 par Ketur » 30 Sep 2012, 20:53
par Ketur » 30 Sep 2012, 20:53
ThekamikazeFou a écrit:exacte et

Donc j'arrive à

et donc à
(x+x_2))
mais je ne vois pas par quoi je peux remplacer

et

.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 30 Sep 2012, 21:00
par ThekamikazeFou » 30 Sep 2012, 21:00
Ketur a écrit:Donc j'arrive à

et donc à
(x+x_2))
mais je ne vois pas par quoi je peux remplacer

et

.

et x reste x, il s'agit de la variable.
-
Ketur
- Messages: 9
- Enregistré le: 30 Sep 2012, 19:59
-
 par Ketur » 30 Sep 2012, 21:01
par Ketur » 30 Sep 2012, 21:01
ThekamikazeFou a écrit: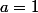
et x reste x, il s'agit de la variable.
Est-ce que ça peut être
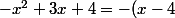(x+1))
car
=a(x-x_1)(x+x_2))
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 30 Sep 2012, 21:02
par ThekamikazeFou » 30 Sep 2012, 21:02
oui c'est correcte, enfin dans la théorie, je n'ai pas vérifier tes calculs mais ils m'ont l'air correct.
-
Ketur
- Messages: 9
- Enregistré le: 30 Sep 2012, 19:59
-
 par Ketur » 30 Sep 2012, 21:16
par Ketur » 30 Sep 2012, 21:16
ThekamikazeFou a écrit:oui c'est correcte, enfin dans la théorie, je n'ai pas vérifier tes calculs mais ils m'ont l'air correct.
Merci :we: ! Et donc j'ai une dernière question qui est En déduire une expression simplifiée de
)
. Est-elle valable pour tout réel

? (Sachant que l'énoncé principale étais "Soit
 = \frac{-x^2+3x+4}{x+1})
pour

.
J'ai mis " Donc
 = \frac{-(x-4)(x+1)}{x+1})
.
)
n'est pas valable pour tout réel

car
(-1+1)}{-1+1} = \frac{-(-5)(0)}{0})
or, on ne peut diviser par 0.
-
ThekamikazeFou
- Membre Relatif
- Messages: 403
- Enregistré le: 12 Juin 2012, 15:26
-
 par ThekamikazeFou » 30 Sep 2012, 21:23
par ThekamikazeFou » 30 Sep 2012, 21:23
oui f(x) et valable pour tout x différent de -1
-
Ketur
- Messages: 9
- Enregistré le: 30 Sep 2012, 19:59
-
 par Ketur » 30 Sep 2012, 21:32
par Ketur » 30 Sep 2012, 21:32
ThekamikazeFou a écrit:oui f(x) et valable pour tout x différent de -1
MERCIII !!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités