Formule a demontrer
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cendrillon
- Membre Relatif
- Messages: 102
- Enregistré le: 29 Mar 2009, 11:51
-
 par cendrillon » 30 Sep 2012, 12:31
par cendrillon » 30 Sep 2012, 12:31
Bonjour,
Je recherche la demonstration de cette propriete :
det ( u,v ) = |u|.|v|. sin (u,v)
avec (u,v) une base.
Merci pour votre aide.
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 30 Sep 2012, 13:04
par Dlzlogic » 30 Sep 2012, 13:04
Bonjour,
La difficulté, c'est que le produit vectoriel est un produit extérieur.
-
cendrillon
- Membre Relatif
- Messages: 102
- Enregistré le: 29 Mar 2009, 11:51
-
 par cendrillon » 30 Sep 2012, 13:11
par cendrillon » 30 Sep 2012, 13:11
Dlzlogic a écrit:Bonjour,
La difficulté, c'est que le produit vectoriel est un produit extérieur.
Et on doit utiliser le produit vectoriel ?
Je dois peut être utiliser la définition d'angle orienté de vecteurs ? (définition qui ne me revient pas là).
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 30 Sep 2012, 13:19
par Dlzlogic » 30 Sep 2012, 13:19
Je suis pas prof, je ne sais pas ce qu'on doit utiliser, en tout cas, il s'agit là de deux formes du produit vectoriel.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 30 Sep 2012, 15:30
par Luc » 30 Sep 2012, 15:30
cendrillon a écrit:Bonjour,
Je recherche la demonstration de cette propriete :
det ( u,v ) = |u|.|v|. sin (u,v)
avec (u,v) une base.
Merci pour votre aide.
Bonjour,
c'est une définition possible du déterminant.
http://fr.wikipedia.org/wiki/D%C3%A9terminant_%28math%C3%A9matiques%29#D.C3.A9terminant_de_deux_vecteurs_dans_le_plan_euclidienCe qu'il faut montrer, c'est que les deux définitions du déterminant coincident : autrement dit que le déterminant (au sens usuel), de la matrice (a b // c d), à savoir ad-bc, c'est bien l'aire du parallélogramme formé par les vecteurs de coordonnées (a,b) et (c,d)
http://en.wikipedia.org/wiki/Determinant#2-by-2_matrices
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 30 Sep 2012, 20:29
par wserdx » 30 Sep 2012, 20:29
Non, je dirais que c'est bien une propriété qui découle de la définition.
Pour le démontrer, il suffit d'écrire u et v en coordonnées polaires:
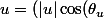, |u| \sin(\theta_u)), v = ( |v| \cos(\theta_v), |v| \sin(\theta_v)))
on a alors
 = |u||v| (\cos(\theta_u) \sin(\theta_v) - \sin(\theta_u)\cos(\theta_v))<br />=|u||v| \sin(\theta_v - \theta_u) = |u||v| \sin(u,v))
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 30 Sep 2012, 20:32
par Luc » 30 Sep 2012, 20:32
wserdx a écrit:Non, je dirais que c'est bien une propriété qui découle de la définition.
Pour le démontrer, il suffit d'écrire u et v en coordonnées polaires:
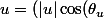, |u| \sin(\theta_u)), v = ( |v| \cos(\theta_v), |v| \sin(\theta_v)))
on a alors
 = |u||v| (\cos(\theta_u) \sin(\theta_v) - \sin(\theta_u)\cos(\theta_v))<br />=|u||v| \sin(\theta_v - \theta_u) = |u||v| \sin(u,v))
Effectivement. La définition à laquelle je faisais référence est l'aire algébrique du parallélogramme formé par les deux vecteurs.
-
cendrillon
- Membre Relatif
- Messages: 102
- Enregistré le: 29 Mar 2009, 11:51
-
 par cendrillon » 30 Sep 2012, 21:27
par cendrillon » 30 Sep 2012, 21:27
wserdx a écrit:Non, je dirais que c'est bien une propriété qui découle de la définition.
Pour le démontrer, il suffit d'écrire u et v en coordonnées polaires:
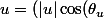, |u| \sin(\theta_u)), v = ( |v| \cos(\theta_v), |v| \sin(\theta_v)))
on a alors
 = |u||v| (\cos(\theta_u) \sin(\theta_v) - \sin(\theta_u)\cos(\theta_v))<br />=|u||v| \sin(\theta_v - \theta_u) = |u||v| \sin(u,v))
Merci wserdx !!! je crois que c'est bien cela que je recherchais


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Oct 2012, 09:39
par chan79 » 02 Oct 2012, 09:39
cendrillon a écrit:Merci wserdx !!! je crois que c'est bien cela que je recherchais

salut
Une autre approche
Soit

l'angle de la rotation qui transforme
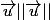
et
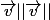
On pose

(x,y) et

(x',y')

on résout alors le système où les inconnues sont
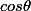
et
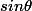
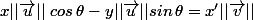
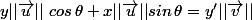
le déterminant est
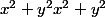
=1
on obtient
cos

=

et
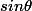
=

la dernière égalité peut s'écrire
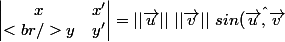
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
