Fonction continue
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ouimet21
- Membre Naturel
- Messages: 94
- Enregistré le: 12 Juin 2010, 03:05
-
 par Ouimet21 » 29 Sep 2012, 19:43
par Ouimet21 » 29 Sep 2012, 19:43
Bonjour,
J'aimerais montrer que la fonction suivante est continue:
=\int_{-\infty}^{\infty} \log(|\frac{x-m}{s}|) \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} dx)
Notons que

et
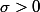
sont fixes.
De plus le domaine de

est

et
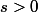
.
Je ne sais pas comment commencer.
Merci.
PS: S'il y a des hypothèses supplémentaires à faire pour que ça soit vrai comme par exemple
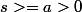
, alors faites les.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 29 Sep 2012, 20:04
par Luc » 29 Sep 2012, 20:04
Bonjour,
il faut que tu regardes et vérifies les hypothèse du théorème qui assure la continuité d'une fonction définie par une intégrale à paramètre. Effectivement, il faudra se placer sur un compact pour s et pour m, pour pouvoir majorer uniformément en s et m la valeur absolue de l'intégrande par une fonction intégrable de x.
Cette fonction est-elle différentiable? de classe C-infinie?
-
Ouimet21
- Membre Naturel
- Messages: 94
- Enregistré le: 12 Juin 2010, 03:05
-
 par Ouimet21 » 29 Sep 2012, 20:24
par Ouimet21 » 29 Sep 2012, 20:24
Luc a écrit:Bonjour,
il faut que tu regardes et vérifies les hypothèse du théorème qui assure la continuité d'une fonction définie par une intégrale à paramètre. Effectivement, il faudra se placer sur un compact pour s et pour m, pour pouvoir majorer uniformément en s et m la valeur absolue de l'intégrande par une fonction intégrable de x.
Cette fonction est-elle différentiable? de classe C-infinie?
Sinon quelqu'un sait comment calculer cette intégrale?
-
Ouimet21
- Membre Naturel
- Messages: 94
- Enregistré le: 12 Juin 2010, 03:05
-
 par Ouimet21 » 29 Sep 2012, 21:56
par Ouimet21 » 29 Sep 2012, 21:56
Personne???
Je ne peux pas me permettre de restreindre le domaine des paramètres à des compacts.
D'ailleurs ce n'est pas une condition nécessaire même pour faire passer la dérivée sous le signe de l'intégrale lorsqu'on utilise le théorème de la moyenne et la convergence dominée.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 02 Oct 2012, 10:28
par arnaud32 » 02 Oct 2012, 10:28
premiere chose, as tu verifier que ta fonction est bien definie?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités