Opération sur n!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 14:15
par sleepy » 29 Sep 2012, 14:15
Bonjour,
Dans un DM, je dois démontrer que

mais je n'arrive pas du tout à démontrer l'autre partie de l'inégalité.
J'aurais donc besoin d'un peu d'aide, s'il vous plait.
Merci d'avance.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 14:37
par Kikoo <3 Bieber » 29 Sep 2012, 14:37
Yop !
Comme ça, je crois qu'une démo de front ne fera pas l'affaire, il faudra une preuve par récurrence.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 29 Sep 2012, 14:37
par nodjim » 29 Sep 2012, 14:37
sleepy a écrit:Bonjour,
Dans un DM, je dois démontrer que

mais je n'arrive pas du tout à démontrer l'autre partie de l'inégalité.
J'aurais donc besoin d'un peu d'aide, s'il vous plait.
Merci d'avance.
Et si tu développais un peu l'écriture ? ça te permettrait de simplifier les termes identiques en haut et en bas.
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 14:38
par sleepy » 29 Sep 2012, 14:38
Il ne faut pas faire de récurrence d'après l'énoncé. Et je n'ai jamais travaillé avec les factorielles donc je ne vois pas comment simplifier ça...
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 14:49
par Kikoo <3 Bieber » 29 Sep 2012, 14:49
Bon ben alors tu fais comme Nodjim.
Alors il est facile de voir que :
\times...\times 2\times 1}{n\times n\times n...\times n})
On simplifie par n en haut et en bas. On remarque qu'il reste n-1 termes en haut et en bas, avec :
[CENTER]



[/CENTER]
On rassemble ainsi :
\times(n-2)\times...\times 2}{n\times n\times...\times n}\times\frac{1}{n})
Le gros produit est inférieur à 1 en vertu des inégalités données donc nous avons bien la conclusion.
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 15:06
par sleepy » 29 Sep 2012, 15:06
Ben .. le gros produit est inférieur à 1, mais on arrive pas à la conclusion.
La tu prouves que

-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 15:11
par Kikoo <3 Bieber » 29 Sep 2012, 15:11
sleepy a écrit:Ben .. le gros produit est inférieur à 1, mais on arrive pas à la conclusion
Euh je suis désolé de te décevoir mais si ! ^^' N'est-ce pas une évidence sachant que n est positif ?
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 15:14
par sleepy » 29 Sep 2012, 15:14
Tu prouves que

C'est bien ça que tu prouves nan?
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 15:29
par sleepy » 29 Sep 2012, 15:29
Or il faut prouver que

-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 15:31
par Kikoo <3 Bieber » 29 Sep 2012, 15:31
Ne lis-tu pas ce que j'ai marqué ?
Le gros produit désigne la fraction de gauche, multipliée par

. Mais j'avoue ne pas avoir été clairissime. Mea culpa.
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 15:36
par sleepy » 29 Sep 2012, 15:36
La je ne comprends pas.
Tu as démontré que

C'est bien ça?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 15:42
par Kikoo <3 Bieber » 29 Sep 2012, 15:42
sleepy a écrit:La je ne comprends pas.
Tu as démontré que

C'est bien ça?
Non,
J'ai donné
!}{n^{n-1}}=\underbrace{\frac{(n-1)!}{n^{n-2}}}_{\mathrm{produit\, de\, n-2\, termes}}\times \frac{1}{n}\leq \frac{1}{n})
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 16:05
par sleepy » 29 Sep 2012, 16:05
J'ai un peu de mal.. tu pourrais rééxpliquer plus en détail s'il te plait?
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 16:13
par sleepy » 29 Sep 2012, 16:13
Est ce que c'est bon si je dis :
}\times\frac{1}{n}=\frac {(n-1)!}{n^(n-2)} \times \frac {1}{n}.)
Or
!}{n^(n-2)} < 1)
Donc
!}{n^(n-2)} \times \frac {1}{n} < \frac {1}{n})
C'est à dire

-
Anonyme
 par Anonyme » 29 Sep 2012, 16:18
par Anonyme » 29 Sep 2012, 16:18
@sleepy et Kikoo <3 Bieber
C'est quasi-évident si on change

par

car
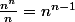
( donc

avec

termes )
et
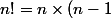 \times (n-2) ... \times 1)
avec

termes dont un des termes est égal à 1
donc on peut considérer qu'il y a aussi  termes
termes
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 16:23
par Kikoo <3 Bieber » 29 Sep 2012, 16:23
Il faut juste que tu voies que
!}{n^{n-2}})
vaut le produit de n-2 fractions dont le numérateur est inférieur au dénominateur. Le tout sera donc inférieur à 1.
-
Anonyme
 par Anonyme » 29 Sep 2012, 16:33
par Anonyme » 29 Sep 2012, 16:33
Superbe conclusion
Question supplémentaire :
faut il faire une démonstration par récurrence pour démontrer cette propriété ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 16:35
par Kikoo <3 Bieber » 29 Sep 2012, 16:35
ptitnoir a écrit:Question supplémentaire :
faut il faire une démonstration par récurrence pour démontrer cette propriété ?
C'est de la philo c'te question :mur:
Oui si on veut de la facilité mais une rédaction plus longue.
Non si on ne sait pas faire une récurrence ou parce qu'on souhaite être plus astucieux.
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 16:57
par sleepy » 29 Sep 2012, 16:57
C'est dur quand même pour une T°S. ^^
En espérant avoir mon cinquième 20 en maths de l'année ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
mais je n'arrive pas du tout à démontrer l'autre partie de l'inégalité.