Racine carré et puissance by feilong

[feilong]

bonsoir
j'ai à résoudre ceci (2V5)2 + 3(2V5)-10 cependant je doute de mon résultat !
c'est 2racine de 5 au carré ! je ne savais pas l' écrire!

et là voici mes calculs
4V25 + 6V5 - 10
= 4V5 + 6V5 -10
= 10V5 - 10

mon raisonnement est-il correct? merci à vous

[ThekamikazeFou]

non c'est faux, je ne sais pas en qu'elle classe tu es donc je vais essayer de t'expliquer cela clairement et simplement.

prenons (2V5)² cela signifie que(2*V5)² donc 2²*V5²
si a>= 0 une racine carré au carré est égale au nombre dans la racine, soit Va² = a

donc 2²*V5² = 4 * 5 = 20

sinon le reste était correcte.

[feilong]

non c'est faux, je ne sais pas en qu'elle classe tu es donc je vais essayer de t'expliquer cela clairement et simplement.

prenons (2V5)² cela signifie que(2*V5)² donc 2²*V5²
si a>= 0 une racine carré au carré est égale au nombre dans la racine, soit Va² = a

donc 2²*V5² = 4 * 5 = 20

sinon le reste était correcte.

oui merci je comprend mieux j'ai fais une erreur donc je rectifie mes calculs
20+6V5-10
= 10 + 6V5

mais j'ai une question si on a V(-a)2 cela donne t'il = -a ou a??

[ThekamikazeFou]

si a>= 0 une racine carré au carré est égale au nombre dans la racine, soit Va² = a

dans une racine a ne peut pas être inférieur à 0, regarde par toi même sur une calculatrice tu verra que cela n'existe pas dans les nombres réels. donc V-a n'existe pas.
si tu sais ce qu'est une fonction, le fonctione Vx est définis à partir de 0 .

[feilong]

dans une racine a ne peut pas être inférieur à 0, regarde par toi même sur une calculatrice tu verra que cela n'existe pas dans les nombres réels. donc V-a n'existe pas.
si tu sais ce qu'est une fonction, le fonctione Vx est définis à partir de 0 .

j'ai demandé çà car j'ai un exercice du type V(-7)2 à résoudre dont je n'arrive pas!
Comment fait-on pour poster une image ? comme çà je pourrais vous faire voir! quand je clique sur l'icône çà m'ouvre un encadré où il faut entrer un texte?

[ThekamikazeFou]

V(-7)² ne peut pas exister, voici la fonction de Vx :



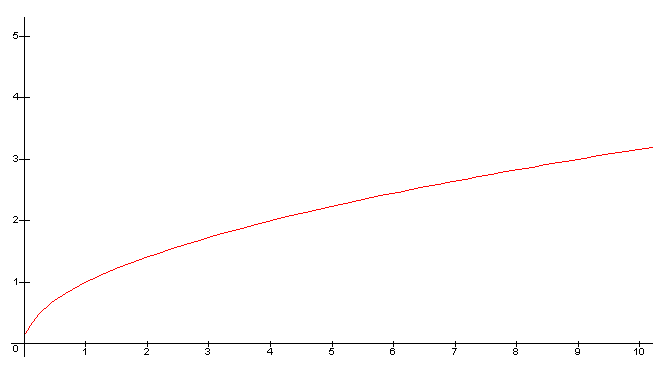
tu vois bien que pour X < 0 (sur l'axe des abscisses ( l'axe horizontale) il n'y a pas de valeur de Vx )


pour mettre une image upload la ici par exemple
http://www.imagup.com/

et utilise la balise [IMG] [ /IMG]

[feilong]

V(-7)² ne peut pas exister, voici la fonction de Vx :



tu vois bien que pour X < 0 (sur l'axe des abscisses ( l'axe horizontale) il n'y a pas de valeur de Vx )


pour mettre une image upload la ici par exemple
http://www.imagup.com/

et utilise la balise [IMG] [ /IMG]

J'ai réussi à résoudre entre temps l'exercice avec V(-7)2 et effectivement çà n'existe pas.
Là je suis sur un nouveau problème (3x-1)2 "au carré" +3(1-3x) (x+2)

je ne sais pas comment commencer! dois je utiliser la formule a2 - 2ab+b2 pour (3x-1)2 ou l'écrire comme (3x-1) (3x-1) +3-9x +x+2 ?????

[feilong]

(3x-1)2 "au carré" +3(1-3x) (x+2)

est ce que je dois procéder comme ceci:

(3x-1) (3x-1) + 3-9x +x+2
= 9x2-3x-3x+1+3-9x+x+2
= 9x2-14x+6
est ce c'est bon?????

[ThekamikazeFou]

(3x-1)2 "au carré" +3(1-3x) (x+2)

qu'elle est t'as question?
tu dois résoudre (3x-1)2 "au carré" +3(1-3x) (x+2) = 0 ?
si oui connais tu es identités remarquables? (3x-1)² + 3(1-3x)(x+2) = 0
(a-b)² = a²-2ab + b²

donc tu développe et ça devrais ce simplifier, ton calcul est faux, vu la forme de l'équation on devrait ne plus avoir de x²

[feilong]

si oui connais tu es identités remarquables? (3x-1)² + 3(1-3x)(x+2) = 0
(a-b)² = a²-2ab + b²

donc tu développe et ça devrais ce simplifier, ton calcul est faux, vu la forme de l'équation on devrait ne plus avoir de x²

la 1ère ligne dont-elle çà?
9x2-2 x 3x1+1 +3-9x +x +2 ?

[ThekamikazeFou]

si oui connais tu es identités remarquables? (3x-1)² + 3(1-3x)(x+2) = 0
(a-b)² = a²-2ab + b²

donc tu développe et ça devrais ce simplifier, ton calcul est faux, vu la forme de l'équation on devrait ne plus avoir de x²

la 1ère ligne dont-elle çà?
9x2-2 x 3x1+1 +3-9x +x +2 ?

non,
(3x-1)² + 3(1-3x)(x+2) = 0
(9x² -6x +1) + 3( x + 2 - 3x² - 6x) = 0
9x² -6x +1 +3x + 6 - 9x² -18x = 0
les x² se supprime.
on a maintenant
-21x + 7 = 0

Ton problème à mon avis, c'est que tu "saute" trops d'étape, pose tout les calcules nécessaire et tu trouvera le bon résultat.

[feilong]

non,
(3x-1)² + 3(1-3x)(x+2) = 0
(9x² -6x +1) + 3( x + 2 - 3x² - 6x) = 0
9x² -6x +1 +3x + 6 - 9x² -18x = 0
les x² se supprime.
on a maintenant
-21x + 7 = 0

Ton problème à mon avis, c'est que tu "saute" trops d'étape, pose tout les calcules nécessaire et tu trouvera le bon résultat.

merci oui c'est vrai j'ai fais des erreurs j'ai développé 3 avec (1-3x) j'ai eu un doute à developper (1-3x) avec (x+2)
merci encore