Equivalent
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
bsangoku
- Membre Relatif
- Messages: 135
- Enregistré le: 09 Jan 2010, 09:05
-
 par bsangoku » 28 Sep 2012, 18:02
par bsangoku » 28 Sep 2012, 18:02
Bonjour,
Je suis actuellement étudiant en M2 et je souhaite savoir comment on a fait pour trouver l'équivalent suivant:
(1-F(x))*sum(F(x), de k=0 à n-1) est équivalent à nF(x).
Merci d'avance
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 28 Sep 2012, 18:10
par Luc » 28 Sep 2012, 18:10
bsangoku a écrit:Bonjour,
Je suis actuellement étudiant en M2 et je souhaite savoir comment on a fait pour trouver l'équivalent suivant:
(1-F(x))*sum(F(x), de k=0 à n-1) est équivalent à nF(x).
Merci d'avance
Bonjour,
quelle est la définition de F et dans quel ensemble est défini x ?
-
bsangoku
- Membre Relatif
- Messages: 135
- Enregistré le: 09 Jan 2010, 09:05
-
 par bsangoku » 28 Sep 2012, 18:14
par bsangoku » 28 Sep 2012, 18:14
F est une fonction de répartition d'une variable X.
-
Anonyme
 par Anonyme » 28 Sep 2012, 18:16
par Anonyme » 28 Sep 2012, 18:16
@bsangoku
Comme dans sum(F(x), de k=0 à n-1 , il n'y a pas de k
on a une somme de n termes identiques donc sum(F(x), de k=0 à n-1= nF(x)
et donc ta formule est fausse ou ton énoncé est incomplet
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 28 Sep 2012, 18:16
par Luc » 28 Sep 2012, 18:16
bsangoku a écrit:F est une fonction de répartition d'une variable X.
Ah, ok.
Et on suppose quelque chose sur la loi de X?
Un autre truc bizarre est que le terme général de la somme ne dépend pas de k.
-
bsangoku
- Membre Relatif
- Messages: 135
- Enregistré le: 09 Jan 2010, 09:05
-
 par bsangoku » 28 Sep 2012, 18:21
par bsangoku » 28 Sep 2012, 18:21
ah non c'est la sum de F(x)^k de k=0 à n-1, désolé
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 28 Sep 2012, 18:30
par Luc » 28 Sep 2012, 18:30
bsangoku a écrit:ah non c'est la sum de F(x)^k de k=0 à n-1, désolé
Si x est un nombre réel fixé, le résultat me paraît faux.
On a une somme géométrique, donc l'égalité se traduit en
^n \sim nF(x))
-
bsangoku
- Membre Relatif
- Messages: 135
- Enregistré le: 09 Jan 2010, 09:05
-
 par bsangoku » 28 Sep 2012, 18:51
par bsangoku » 28 Sep 2012, 18:51
Luc a écrit:Si x est un nombre réel fixé, le résultat me paraît faux.
On a une somme géométrique, donc l'égalité se traduit en
^n \sim nF(x))
Je n'ai pas compris ta remarque, car
(1-F(x))*sum(F(x)^k, de k=0 à n-1)= 1-F(x)
D'autre part, en quoi c'est normal dans le cas d'une somme géométriique?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 28 Sep 2012, 19:02
par Luc » 28 Sep 2012, 19:02
bsangoku a écrit:Je n'ai pas compris ta remarque, car
(1-F(x))*sum(F(x)^k, de k=0 à n-1)= 1-F(x)
D'autre part, en quoi c'est normal dans le cas d'une somme géométriique?
La somme
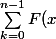^k)
est géométrique, donc vaut
^n}{1-F(x)})
-
Anonyme
 par Anonyme » 29 Sep 2012, 08:35
par Anonyme » 29 Sep 2012, 08:35
Luc a écrit:La somme
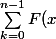^k)
est géométrique, donc vaut
^n}{1-F(x)})
Il faut ajouter : pour tous les

tels que
 \ne 1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
