Nombre de diviseurs d'un entier

[BiZi]

Bonjour,

Soit n un entier naturel non nul.

On a n=p1^(k1)*p2^(k2)*...*pi^(ki), avec p1,p2,...pi des nombres premiers,
et k1,k2,...,ki des entiers naturels non nuls (décomposition en facteurs premiers).

Comment peut-on exprimer le nombre de diviseurs de n en fonction de i et k1,k2,...,ki?

Merci d'avance!

(ki ne représente pas le prduit k*i, mais il faut lire k indice i)

[BiZi]

Euh en fait c'est évidemment (k1+1)*(k2+1)*...*(kn+1)...

Je viens de trouver et dire que je cherchais des trucs super compliqués :marteau:

Bon j'efface pas la discussion ca pourra toujours servir à quelqu'un :we: .

[aviateurpilot]

une petite question
cherche le produit des diviseurs :++:

[aviateurpilot]

soit , les p-k son des nombres premiers
un diviseur d de n est de la forme avec
puisque pour chaque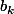 il y a a_k+1 choix
donc le nombre de divieurs est

le produit des diviseurs est
avec la somme des valeur possible de et 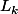le nombre de diviseur de
donc le produit des diviseurs est
et on trouve facilement que queque soit k ;nombre de diviseur de n=d(n)
par suite on trouve == donc c'est

[aviateurpilot]

qui confirme?

[nekros]

Vérifie ton résultat avec un exemple concret (prend n=?)

Thomas G :zen:

[aviateurpilot]

je veus une confirmation de ce que j'ai fait pour trouver la relation

[Amine.MASS]

je veus une confirmation de ce que j'ai fait pour trouver la relation

moi je confirme c que tu as dis (même si ça manque de rigueur,mais je te félicite)
voilà je te propose une autre methode plus simple:
(Rq: veut dire le produit sur les diviseurs de n)
donc:



d'ou le resultat que tu as trouvé :++:

[aviateurpilot]

merci amine