(a)^{n}-(b)^{n}
19 messages
- Page 1 sur 1
(a)^{n}-(b)^{n}
pour retrouver le résultat de (a)^{n}-(b)^{n} on procède par récurrence sinon qui pourrait me donner une autre méthode
Ups faute de frappe mais la reponse que t'as donné et fausse aussi si le compteur k démarre 0 il ira jusqu'à n-1 de a^n-k-1 * b^k et s'il demarre de 1 il ira jusqu'à n de a^n-k * b^k-1 de toutes façon il ya n termes dans la somme d'autres part j'ai une demonstration qui est un peu longue ! J'ai mis cette question afin d'avoir une demonstration plus courtte mais il parait qu'il y'en a pas !
Commençant par calculer 1-x^n = (1+x+x^2+...+x^n-1) - (x+x^2+...+x^n) ça donne Somme de k=0 à n-1 de x^k moin somme de k=1 à n de x^k on remettra les deux sommes sous le meme comteur donc la deuxieme somme deviend la somme de k=0 à n-1 de x^(k+1) on ura ainsi 1-x^n= S k=0 à n-1 de x^k * (1-x) , on fait sortir 1-x de la somme et on aura le resultat 1-x^n = (1-x)* S de k=0 à n-1 de x^k pour a^n - b^n il suffit de supposer que a est non nul ( sinon le resultat est evident ) et de factoriser par a^n on aura a^n -b^n = a^n (1-(b/a)^n ) on applique la 1ére demonstration sur 1-(a/b)^n et on aura le resultat que j'ai mis
Commençant par calculer 1-x^n = (1+x+x^2+...+x^n-1) - (x+x^2+...+x^n) ça donne Somme de k=0 à n-1 de x^k moin somme de k=1 à n de x^k on remettra les deux sommes sous le meme comteur donc la deuxieme somme deviend la somme de k=0 à n-1 de x^(k+1) on ura ainsi 1-x^n= S k=0 à n-1 de x^k * (1-x) , on fait sortir 1-x de la somme et on aura le resultat 1-x^n = (1-x)* S de k=0 à n-1 de x^k pour a^n - b^n il suffit de supposer que a est non nul ( sinon le resultat est evident ) et de factoriser par a^n on aura a^n -b^n = a^n (1-(b/a)^n ) on applique la 1ére demonstration sur 1-(a/b)^n et on aura le resultat que j'ai mis
trois-demis a écrit:Ups faute de frappe mais la reponse que t'as donné et fausse aussi si le compteur k démarre 0 il ira jusqu'à n-1 de a^n-k-1 * b^k et s'il demarre de 1 il ira jusqu'à n de a^n-k * b^k-1 de toutes façon il ya n termes dans la somme d'autres part j'ai une demonstration qui est un peu longue ! J'ai mis cette question afin d'avoir une demonstration plus courtte mais il parait qu'il y'en a pas !
Commençant par calculer 1-x^n = (1+x+x^2+...+x^n-1) - (x+x^2+...+x^n) ça donne Somme de k=0 à n-1 de x^k moin somme de k=1 à n de x^k on remettra les deux sommes sous le meme comteur donc la deuxieme somme deviend la somme de k=0 à n-1 de x^(k+1) on ura ainsi 1-x^n= S k=0 à n-1 de x^k * (1-x) , on fait sortir 1-x de la somme et on aura le resultat 1-x^n = (1-x)* S de k=0 à n-1 de x^k pour a^n - b^n il suffit de supposer que a est non nul ( sinon le resultat est evident ) et de factoriser par a^n on aura a^n -b^n = a^n (1-(b/a)^n ) on applique la 1ére demonstration sur 1-(a/b)^n et on aura le resultat que j'ai mis
Effectivement, k va de 0 à n-1.
Preuve par récurrence :
Soient a,b réels. Montrons par récurrence que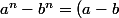\sum_{k=0}^{n-1}a^kb^{n-1-k})
Pour n=0, c'est vrai.
Soit n entier tel que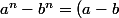 \sum_{k=0}^{n-1}a^kb^{n-1-k}) .
.
Alors \sum_{k=0}^{n}a^kb^{n-k}=(a-b)(\sum_{k=0}^{n-1}a^kb^{n-k}+a^n)=(a-b)(b\sum_{k=0}^{n-1}a^kb^{n-1-k}+a^n)=b(a^n-b^n)+(a-b)a^n) par hypothèse de récurrence.
par hypothèse de récurrence.
Donc \sum_{k=0}^{n}a^kb^{n-k}=a^{n+1}+ba^n-ba^n-b^{n+1}=a^{n+1}-b^{n+1}) , d'où l'hérédité, ce qui clôt la récurrence.
, d'où l'hérédité, ce qui clôt la récurrence.
Preuve directe : Soit entier fixé.
entier fixé.
\sum_{k=0}^{n-1}a^kb^{n-1-k}=\sum_{k=0}^{n-1}a^{k+1}b^{n-(k+1)}-\sum_{k=0}^{n-1}a^kb^{n-k}=\sum_{k=1}^{n}a^kb^{n-k}-\sum_{k=0}^{n-1}a^kb^{n-k}=a^n-b^n) (tous les termes de la somme s'annulent sauf pour
(tous les termes de la somme s'annulent sauf pour 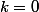 et
et 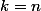 ).
).
La preuve directe est préférable, plus courte. La récurrence est une fausse bonne idée.
Soient a,b réels. Montrons par récurrence que
Pour n=0, c'est vrai.
Soit n entier tel que
Alors
Donc
Preuve directe : Soit
La preuve directe est préférable, plus courte. La récurrence est une fausse bonne idée.
Luc a écrit:Preuve par récurrence :
Soient a,b réels. Montrons par récurrence que
Pour n=0, c'est vrai.
Soit n entier tel que.
Alorspar hypothèse de récurrence.
Donc, d'où l'hérédité, ce qui clôt la récurrence.
Preuve directe : Soitentier fixé.
(tous les termes de la somme s'annulent sauf pour
et
).
La preuve directe est préférable, plus courte. La récurrence est une fausse bonne idée.
La somme
Sa somme vaut
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
