Suite, démontrer qu'elle est croissante

par **constantinowitch** » 26 Sep 2012, 17:02

Bonjour je suis en terminale et je dois démontrer que :
U(n+1)>U(n)

Je sais que U(n+1)=racine carré de (3*U(n) +4)

Donc racine carré de (3*U(n) +4) - U(n) >0
Donc equivaut à [3*U(n) + 4]^(1/2) - U(n)

Que faire avec ça ? :help:

PS La suite est majoré par 4.

Merci.

par **Luc** » 26 Sep 2012, 17:21

Salut,

tu peux étudier la fonction f définie par

et regarder son signe.

par **Joker62** » 26 Sep 2012, 17:26

Sinon par récurrence ça marche bien.

par **constantinowitch** » 26 Sep 2012, 17:32

La dérivé de cette fonction c'est bien :

?

par **chan79** » 26 Sep 2012, 17:35

constantinowitch a écrit:Bonjour je suis en terminale et je dois démontrer que :
U(n+1)>U(n)

Je sais que U(n+1)=racine carré de (3*U(n) +4)

Donc racine carré de (3*U(n) +4) - U(n) >0
Donc equivaut à [3*U(n) + 4]^(1/2) - U(n)

Que faire avec ça ? :help:

PS La suite est majoré par 4.

Merci.

salut
pas d'info sur u(0) ?

par **Luc** » 26 Sep 2012, 17:44

constantinowitch a écrit:La dérivé de cette fonction c'est bien : ?

Presque, mais tu as oublié un facteur 3 quand tu as dérivé

par **constantinowitch** » 26 Sep 2012, 18:00

Hein ? Un facteur de trois ?

par **Joker62** » 26 Sep 2012, 18:06

La dérivée de racine(u) doit arriver plus tard dans le cours.

Fais le par récurrence

par **constantinowitch** » 26 Sep 2012, 18:10

J'ai essayé mais là je retombe sur le problème de : quesque je fais avec la racine ?

par **Joker62** » 26 Sep 2012, 18:14

écris ta récurrence ici pour voir :)

par **Luc** » 26 Sep 2012, 18:19

constantinowitch a écrit:Hein ? Un facteur de trois ?

C'est juste que la dérivée de la fonction vaut

et non

.

La dérivée de

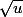
est

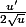
. Tu avais oublié le

.

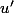
par **constantinowitch** » 26 Sep 2012, 18:19

P(n) : << U(n) < U(n+1) >> vraie pour P(0)

Par HR U(n) < U(n+1)
Donc 0 < U(n+1) -U(n)

Je sais que U(n+1)=racine carré de (3*U(n) +4)

Donc racine carré de (3*U(n) +4) - U(n) >0
Donc equivaut à [3*U(n) + 4]^(1/2) - U(n) > 0

Et je fais quoi ?

par **Luc** » 26 Sep 2012, 18:21

constantinowitch a écrit:P(n) : > vraie pour P(0)

Par HR U(n) 0
Donc equivaut à [3*U(n) + 4]^(1/2) - U(n) > 0

Et je fais quoi ?

Dans une récurrence, que supposes-tu, et que veux-tu montrer? Le raisonnement logique n'est pas très clair quand on te lit.

par **constantinowitch** » 26 Sep 2012, 18:44

Oh que je suis stupide. Pourquoi voulais-je transformer U(n+1).
Merci de m'avoir ouvert les yeux, il suffisait de faire une série d'opération pour tomber sur U(n+1) < U(n+2)

par **Joker62** » 26 Sep 2012, 19:35

Pour conclure encore plus rapidement qu'avec une série d'opérations, on a :

u(x) = 3x+4 et v(x) = Racine(3x+4) ont les mêmes variations (théorème de 1ère)

Donc v(x) = racine(3x+4) est croissante sur son ensemble de définition.

par **Anonyme** » 27 Sep 2012, 09:58

sans la valeur de

cela va être difficile de conclure....

PS)
Ne pas oublier de préciser que cette suite est bien définie car c'est une suite positive

Suite, démontrer qu'elle est croissante

Suite, démontrer qu'elle est croissante

Qui est en ligne