Infiniment petit
18 messages
- Page 1 sur 1
Infiniment petit
Bonjour, je ne comprend pas bien l'énoncé de cet exercice :
Pour tous a,b, on note :
fa,b(x) = exp(x) - [ (1+ax)/(1+bx)]
Déterminer les nombres a et b tels que fa,b(x) est un infiniment petit d'ordre maximum quand x->0 et donnez un équivalent.
Que veut dire infiniment petit d'ordre maximum ? je n'ai pas de definition dans mon cours.
Je pense qu'il faut ecrire f = o(x^n) avec x-> 0 mais je ne vois pas trop.
Merci de m'expliquer
Pour tous a,b, on note :
fa,b(x) = exp(x) - [ (1+ax)/(1+bx)]
Déterminer les nombres a et b tels que fa,b(x) est un infiniment petit d'ordre maximum quand x->0 et donnez un équivalent.
Que veut dire infiniment petit d'ordre maximum ? je n'ai pas de definition dans mon cours.
Je pense qu'il faut ecrire f = o(x^n) avec x-> 0 mais je ne vois pas trop.
Merci de m'expliquer
wserdx a écrit:Procède par étapes. Commence parpuis
puis
.
D'accord pour le DL, j'utilise la formule de (1+x)^-1, je viens de comprendre mais ce que je comprends mais c'est une fois que j'aurai la formule du Dl de f,
On m'a dit : Il faut choisir les valeurs de a et b qui annulent le ou les premiers termes du DL
Je ne comprends pas bien comment savoir le quels doivent s'annuler ???
Désolé, je n'ai pas été clair. Un développement limité est une expression polynomiale terminée par un infiniment petit, plus "petit" que le polynôme. Mais chaque terme du polynôme peut être vu comme un infiniment petit, par rapport aux termes qui le précèdent à condition de les ranger par ordre de "prépondérance", c'est-à-dire le terme constant d'abord, puis les termes en  ,
,  etc.
etc.
Dans cet exercice on te demande de faire en sorte que l'ordre du développement soit maximum, c'est-à-dire que le premier terme non nul du développement soit de degré le plus élevé possible.
Donc il faut absolument calculer le terme constant, le terme en ,
,  , etc. en fonction de a et b, et écrire les équations qui annulent ces différents coefficients.
, etc. en fonction de a et b, et écrire les équations qui annulent ces différents coefficients.
Commence par faire un développement à l'ordre 2.
Dans cet exercice on te demande de faire en sorte que l'ordre du développement soit maximum, c'est-à-dire que le premier terme non nul du développement soit de degré le plus élevé possible.
Donc il faut absolument calculer le terme constant, le terme en
Commence par faire un développement à l'ordre 2.
Merci beaucoup pour l'aide que vous m"apporter car je n'ai jamais utilisé les infiniment petit du coup j'ai vraiment du mal.
A l'ordre 2 :
fa,b(x) = 1 + x + x²/2! + (1+ax)(1-bx+bx²) + o(x²)
= 1 + x + x²/2! + 1 -bx + bx² +ax -bax² + bax^3 + o(x²)
J'enlève le bax^3 qui dépasse le degré 2
= 1 + x(a-b) + x²( 1/2! + b ) + o(x²)
a-b = 0 donne a = b ce qui annule le terme en x
b = -1/2! annule aussi le terme en x²
Est ce exact ?
Il faudrait que je fasse cela à l'ordre n ????
A l'ordre 2 :
fa,b(x) = 1 + x + x²/2! + (1+ax)(1-bx+bx²) + o(x²)
= 1 + x + x²/2! + 1 -bx + bx² +ax -bax² + bax^3 + o(x²)
J'enlève le bax^3 qui dépasse le degré 2
= 1 + x(a-b) + x²( 1/2! + b ) + o(x²)
a-b = 0 donne a = b ce qui annule le terme en x
b = -1/2! annule aussi le terme en x²
Est ce exact ?
Il faudrait que je fasse cela à l'ordre n ????
Oups, une petite erreur de recopie.
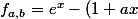/(1+bx))
du coup le DL devient (mais je te laisse revérifier les calculs)
+x^2 (a b-b^2+1/2)+x^3 (-a b^2+b^3+1/6)+O(x^4))
(J'utilise wolfram alpha en ligne, je ne suis plus payé pour faire ce genre de calculs à la main...)
Donc si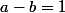 , tu annules le premier terme
, tu annules le premier terme
Si=-1/2) , tu annules le deuxième terme,
, tu annules le deuxième terme,
Si=1/6) , tu annules le troisième terme, etc.
, tu annules le troisième terme, etc.
Tu devrais trouver une ou des solutions communes aux deux premières équations, mais pas de solutions si tu considères les 3 premières équations simultanées...
du coup le DL devient (mais je te laisse revérifier les calculs)
(J'utilise wolfram alpha en ligne, je ne suis plus payé pour faire ce genre de calculs à la main...)
Donc si
Si
Si
Tu devrais trouver une ou des solutions communes aux deux premières équations, mais pas de solutions si tu considères les 3 premières équations simultanées...
wserdx a écrit:Oups, une petite erreur de recopie.
du coup le DL devient (mais je te laisse revérifier les calculs)
(J'utilise wolfram alpha en ligne, je ne suis plus payé pour faire ce genre de calculs à la main...)
Donc si, tu annules le premier terme
Si, tu annules le deuxième terme,
Si, tu annules le troisième terme, etc.
Tu devrais trouver une ou des solutions communes aux deux premières équations, mais pas de solutions si tu considères les 3 premières équations simultanées...
D'accord mais du coup l'ordre 4 suffit ou il faut que j'aille plus loin ???
Du coup je dois resoudre les 3 equations ensemble ou deux puis une ?
Et du coup quelle est l'équivalents lié ?
Merci pour toute la gentillesse que vous avez à m'aider
Malicia a écrit:D'accord mais du coup l'ordre 4 suffit ou il faut que j'aille plus loin ???
Du coup je dois resoudre les 3 equations ensemble ou deux puis une ?
Et du coup quelle est l'équivalents lié ?
Merci pour toute la gentillesse que vous avez à m'aider
Le problème est d'annuler le maximum de coefficients, mais dans l'ordre.
On essaie d'annuler le premier.
Puis simultanément premier et second.
Puis simultanément premier, 2ème, 3ème. etc.
On sarrête dès qu'on ne peut plus.
j'ai à moitié répondu précédemment : il n'y a pas de solution qui annule simultanément les 3 premiers (vérifie-le!)
Bon courage...
wserdx a écrit:Le problème est d'annuler le maximum de coefficients, mais dans l'ordre.
On essaie d'annuler le premier.
Puis simultanément premier et second.
Puis simultanément premier, 2ème, 3ème. etc.
On sarrête dès qu'on ne peut plus.
j'ai à moitié répondu précédemment : il n'y a pas de solution qui annule simultanément les 3 premiers (vérifie-le!)
Bon courage...
Je viens de le verifier merci donc l'ordre 2 suffit pour annuler tout ca
Mais comment avec cela voit on l'equivalent de f ?
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
