Le nombre √2

[Filly]

Bonjour j'ai un DM a rendre pour la semaine prochaine mais je ne parvient pas à démarrer, voici les 2 premières questions:

On note f la fonction définie sur R*+ par : f(x)= ½ (x+2/x)

1. Montrer que pour tout x appartient à R*+ ; f(x) ;) ;)2

2.Montrer que pour tout x appartient a ];)2;+;)[ ; f(x) ;)x

[Kikoo <3 Bieber]

Bonjour j'ai un DM a rendre pour la semaine prochaine mais je ne parvient pas à démarrer, voici les 2 premières questions:

On note f la fonction définie sur R*+ par : f(x)= ½ (x+2/x)

1. Montrer que pour tout x appartient à R*+ ; f(x) 2

2.Montrer que pour tout x appartient a ];)2;+;)[ ; f(x) x

Salut,

1) Tu analyses f et tu remarques qu'elle admet un minimum en qui vaut... .
2) Sur cet intervalle étudie f(x)-x.

[Filly]

Salut,

1) Tu analyses f et tu remarques qu'elle admet un minimum en qui vaut... .
2) Sur cet intervalle étudie f(x)-x.

Est ce que pour répondre a la question 1 il suffit de calculer le minimum de f?

[Kikoo <3 Bieber]

Est ce que pour répondre a la question 1 il suffit de calculer le minimum de f?

Oui, cela suffit pour montrer que minore f.

[Filly]

Oui, cela suffit pour montrer que minore f.

Je ne parviens pas à faire ce calcul :/

[Kikoo <3 Bieber]

Utilise la linéarité de la dérivation : (f+g)'=f'+g' (noté abusivement, mais t'as compris)

[Filly]

Mais dans ma fonction de départ que sont f et g ?

[Filly]

Je suis vraiment désolée mais je ne comprend rien :/

[Kikoo <3 Bieber]

x et 2/x normalement.

[Filly]

La question va sembler totalement stupide mais est ce que la dérivée de x/2 = 1/2 * x? Et quelle est la dérivée de x ????

[Kikoo <3 Bieber]

x/2=(1/2)x
Or la dérivée de ax=...
Donc...

[Filly]

Je suis totalement perdue ...

[Kikoo <3 Bieber]

Dis, tu es en Terminale S ?

[chan79]

Bonjour j'ai un DM a rendre pour la semaine prochaine mais je ne parvient pas à démarrer, voici les 2 premières questions:

On note f la fonction définie sur R*+ par : f(x)= ½ (x+2/x)

1. Montrer que pour tout x appartient à R*+ ; f(x) 2

2.Montrer que pour tout x appartient a ];)2;+;)[ ; f(x) x

on peut aussi raisonner par équivalence( x estpositif)

½ (x+2/x) équivaut à

x²+2

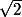
(x- )²

idem pour l'autre

[Filly]

Oui mais j'ai des lacunes énormes à cause d'une année de première difficile ..

[Kikoo <3 Bieber]

Oui mais j'ai des lacunes énormes à cause d'une année de première difficile ..

D'accord,

Je vois que Chan a posté quelque chose de bien valide donc tu peux prendre en note.
Mais on s'attend à ce que tu saches faire ceci en utilisant l'analyse, donc essaie de reprendre calmement tes cours sur les dérivées, limites, etc.

[Filly]

Il n'y a plus du tout de limite au programme de la 1erS, on vient de commencer à les étudier. J'essaie de tout reprendre petit à petit mais c'est assez laborieux :/
Pouvez vous m'aider à raisonner pour trouver le résultat a la premiere question?

Merci Chan79 :)

[Luc]

Bonjour,

as-tu étudié les dérivées l'année dernière?
Si tu ne connais pas les dérivées, l'exercice est possible à résoudre mais il faut s'y prendre autrement. Disons que la connaissance des dérivées permet l'étude de n'importe quelle fonction.

[Filly]

Bonjour,

as-tu étudié les dérivées l'année dernière?
Si tu ne connais pas les dérivées, l'exercice est possible à résoudre mais il faut s'y prendre autrement. Disons que la connaissance des dérivées permet l'étude de n'importe quelle fonction.

Oui j'ai étudié les dérivées

[Kikoo <3 Bieber]

Etudier les dérivées sans voir les limites, je trouve que ça n'a pas trop de sens, car les dérivées sont elles même des notions découlant de celle de limite.
Et on se demande maintenant pourquoi les lycéens ont de plus en plus de mal à comprendre. Normal, on leur parachute tout, et on enlève aussi un peu de choses par-ci, par-là...
Bref, reprends ton tableau de dérivées et fais-le de cette manière si tu veux. Sinon, utilise la méthode de Chan qui établit une vérité mathématique par équivalences successives.