Resolution d' équation by feilong

[feilong]

bonsoir
je suis sur une équation et je bloque :

(4x2 -12x+9) - (4x-6) (3x+1) = 0
C'est 4x au carré......je n'arrive plus à trouver la page expliquant les formules d'écritures!!!
la solution du livre est -3/2 et 5/4
or je n'arrive pas à trouver ce résultat
voici mes calculs

je développe (4x2-12x+9) - (12x2+4x-18x-6)= 0
-8x2+2x+15 = 0
j'utilise ensuite delta qui donne 22 (deux au carré) -4(-8)(15)= 484 soit 22^2

Je ne vois pas comment trouver -3/2 et 5/4 ?????
pouvez vous m'aider svp merci pour toute pistes...... :lol3:

[Luc]

bonsoir
Je ne vois pas comment trouver -3/2 et 5/4 ?????
pouvez vous m'aider svp merci pour toute pistes...... :lol3:

Salut,
Tout est bon jusqu'au calcul de delta compris, ensuite tu calcules les racines

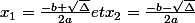
[feilong]

Salut,
Tout est bon jusqu'au calcul de delta compris, ensuite tu calcules les racines

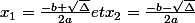
la formule donnée est ce une formule spécifique à delta lorsqu'on a affaire à un racine carré comme résultat?? quand doit-on l' employer? elle s'utilise qu'avec les équations a solutions nulles?? je ne connaissais pas cette formule......

donc cela me donne :
-2+22/ (2x(-8)) = -20/16 = -5/4
-2-22/(2x(-8)) = -24/-16 = 3/2

merci pour votre aide!

[Luc]

Les résultats me paraissent corrects.
La formule que je t'ai donnée est la formule générale de résolution de l'équation du second degré
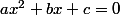
avec non nul (sinon ce n'est pas du second degré).
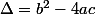
Et comme tu l'as calculé.

[ampholyte]

Les résultats me paraissent corrects.
La formule que je t'ai donnée est la formule générale de résolution de l'équation du second degré
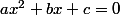
avec non nul (sinon ce n'est pas du second degré).
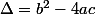
Et comme tu l'as calculé.

Petite précision delta doit être positif ou nul pour calculer les racines avec les formules données plus haut

[feilong]

Petite précision delta doit être positif ou nul pour calculer les racines avec les formules données plus haut

si delta est négatif on a pas recours a cette formule donc?

[feilong]

Les résultats me paraissent corrects.
La formule que je t'ai donnée est la formule générale de résolution de l'équation du second degré
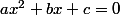
avec non nul (sinon ce n'est pas du second degré).
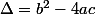
Et comme tu l'as calculé.

OK merci pour les infos !!!! :lol3:

[ampholyte]

OK merci pour les infos !!!! :lol3:

Si delta est négatif on a :

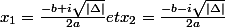
[Luc]

si delta est négatif on a pas recours a cette formule donc?

si delta est négatif, il n'y a pas de racines réelles, mais il y a deux racines complexes conjuguées. (tu verras ça en terminale S)
Edit : grilled :we:

[Black Jack]

Oui mais ...

Je parierais que le but était se s'apercevoir que 4x² - 12x + 9 = (2x-3)² et que donc l'équation pouvait s'écrire :

(2x-3)² - 2(2x-3)(3x+1) = 0

Et puis poursuivre en mettant (2x-3) en facteur ...

:zen:

[feilong]

merci pour vos dernières réponses !
ok pour la formule si delta est négatif