Element de surface en polaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sylwa
- Membre Naturel
- Messages: 32
- Enregistré le: 18 Aoû 2010, 13:49
-
 par sylwa » 19 Sep 2012, 21:43
par sylwa » 19 Sep 2012, 21:43
Bonjour !
Lors du changement de référentiel cartésien vers polaire, le Jacobien vaut r, et par conséquent l'élément de surface polaire est

.
J'ai voulu retrouver cet élément de surface polaire par une méthode plus "intuitive".
En partant du changement de variable habituel :
)
et
)
, il vient :
dr -rsin(\theta)d\theta)
et
dr +rcos(\theta)d\theta)
.
Ainsi dx.dy =
dr -rsin(\theta)d\theta).(sin(\theta)dr +rcos(\theta)d\theta))
En ne gardant que les termes d'ordre 1 en dr et

, on a :
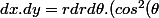-sin^2(\theta)\ \neq\ rdr d\theta)
!
Pourriez vous pointer mon erreur s'il vous plaît !

Merci pour vos suggestions.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 19 Sep 2012, 22:51
par Luc » 19 Sep 2012, 22:51
Je suis aussi passé par la :lol3:
En fait, le produit

est ce qu'on appelle un produit extérieur. Bon, en pratique on se fiche du nom mais il a une propriété très importante : il est antisymétrique!
Du coup

, et on obtient bien le même élément de surface!
De plus,
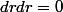
et

: ce n'est pas une "approximation a l'ordre 1", c'est mathématiquement totalement exact par propriété du produit extérieur. (un peu comme le produit vectoriel).
-
sylwa
- Membre Naturel
- Messages: 32
- Enregistré le: 18 Aoû 2010, 13:49
-
 par sylwa » 21 Sep 2012, 10:35
par sylwa » 21 Sep 2012, 10:35
Luc a écrit:Je suis aussi passé par la :lol3:
En fait, le produit

est ce qu'on appelle un produit extérieur. Bon, en pratique on se fiche du nom mais il a une propriété très importante : il est antisymétrique!
Du coup

, et on obtient bien le même élément de surface!
De plus,
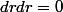
et

: ce n'est pas une "approximation a l'ordre 1", c'est mathématiquement totalement exact par propriété du produit extérieur. (un peu comme le produit vectoriel).
Merci Luc pour ta réponse.
Cela dit, qu'entends tu par produit extérieur, produit vectoriel ?
Si oui, je ne vois pas où intervient le produit extérieur dans le calcul de l'élément de surface polaire.
Pourrais tu expliciter s'il te plaît, j'aimerais bien appliquer cette méthode au cas sphérique par exemple pour vérifier ma compréhension.
Sylvain
-
fal
- Membre Naturel
- Messages: 54
- Enregistré le: 16 Déc 2010, 17:34
-
 par fal » 21 Sep 2012, 11:30
par fal » 21 Sep 2012, 11:30
à mon avis, vos connaissances son t suffisantes!! faut pas chercher midi à 14h
-
Dlzlogic
- Membre Transcendant
- Messages: 5273
- Enregistré le: 14 Avr 2009, 12:39
-
 par Dlzlogic » 21 Sep 2012, 11:45
par Dlzlogic » 21 Sep 2012, 11:45
Bonjour,
Le produit vectoriel donne une valeur qui correspond à l'aire du triangle formé par les 2 vecteurs.
C'est un vecteur normal au plan défini par les deux vecteurs. On se trouve donc dans un espace 3D. Certains auteurs le précisent expressément, ce qui tendrait à créer cette troisième dimension, avec ce que cela entraine pour calculer la valeur numérique d'une aire. Pour mémoire, cette méthode est très employée pour connaitre la position relative de 3 points, c'est à dire si on parcourt le périmètre du triangle ainsi formé, on saura le sens dans lequel on tourne.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 21 Sep 2012, 11:47
par barbu23 » 21 Sep 2012, 11:47
Moi, je suis de l'avis de @fal, mais, si tu veux, on peut faire comme ce qu'a dit @Luc : :happy3:
dr -rsin(\theta)d\theta $)
et
dr +rcos(\theta)d\theta $)
Donc,
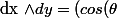dr -rsin(\theta)d\theta ) \wedge ( sin(\theta)dr +rcos(\theta)d\theta ) $)
 \sin ( \theta ) dr \wedge dr + r \cos^2 ( \theta ) dr \wedge d \theta - r \sin^2 ( \theta ) d \theta \wedge dr - r^2 \cos ( \theta ) \sin ( \theta ) d \theta \wedge d \theta $)
Et comme :

et

Alors :
 \sin ( \theta ) dr \wedge dr + r \cos^2 ( \theta ) dr \wedge d \theta + r \sin^2 ( \theta ) dr \wedge d \theta + r^2 \cos ( \theta ) \sin ( \theta ) d \theta \wedge d \theta $)
 + \sin^2 ( \theta ) ) dr \wedge d \theta $)
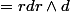
Par conséquent :
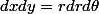
.
-
sylwa
- Membre Naturel
- Messages: 32
- Enregistré le: 18 Aoû 2010, 13:49
-
 par sylwa » 22 Sep 2012, 14:30
par sylwa » 22 Sep 2012, 14:30
barbu23 a écrit:Moi, je suis de l'avis de @fal, mais, si tu veux, on peut faire comme ce qu'a dit @Luc : :happy3:
dr -rsin(\theta)d\theta $)
et
dr +rcos(\theta)d\theta $)
Donc,
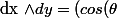dr -rsin(\theta)d\theta ) \wedge ( sin(\theta)dr +rcos(\theta)d\theta ) $)
 \sin ( \theta ) dr \wedge dr + r \cos^2 ( \theta ) dr \wedge d \theta - r \sin^2 ( \theta ) d \theta \wedge dr - r^2 \cos ( \theta ) \sin ( \theta ) d \theta \wedge d \theta $)
Et comme :

et

Alors :
 \sin ( \theta ) dr \wedge dr + r \cos^2 ( \theta ) dr \wedge d \theta + r \sin^2 ( \theta ) dr \wedge d \theta + r^2 \cos ( \theta ) \sin ( \theta ) d \theta \wedge d \theta $)
 + \sin^2 ( \theta ) ) dr \wedge d \theta $)
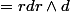
Par conséquent :
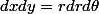
.
Merci beaucoup à vous Dlzlogic et barbu23 pour cet effort très significatif de pédagogie!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
