Singularité (holomorphie)
20 messages
- Page 1 sur 1
Singularité (holomorphie)
Bonjour
j'ai un problème pour la fonction f de C dans C : z -> cos(1/z) + 1/(z*z).
f est donc holomorphe dans C\{0}.
f a une singularité pour z=0
Je voudrais savoir quelle singularité.
Si j'écris le dévellopement en série de cos pour 1/z, j'obtiens la série de Laurent de f. Donc ce serait un point de singularité essentiel.
Mais pourtant, |f(z)| -> l'infini pour z->0 non?
parce que |f(z)|>= cos(bla) + |1/(z*z)| >= -1 + |1/(z*z)| -> infini.
et ça c'est bien la charaktérisation d'un pole, non?
Merci de me dire où est ce que je fais une erreur, et quelle est la bonne solution!
Merci beaucoup
j'ai un problème pour la fonction f de C dans C : z -> cos(1/z) + 1/(z*z).
f est donc holomorphe dans C\{0}.
f a une singularité pour z=0
Je voudrais savoir quelle singularité.
Si j'écris le dévellopement en série de cos pour 1/z, j'obtiens la série de Laurent de f. Donc ce serait un point de singularité essentiel.
Mais pourtant, |f(z)| -> l'infini pour z->0 non?
parce que |f(z)|>= cos(bla) + |1/(z*z)| >= -1 + |1/(z*z)| -> infini.
et ça c'est bien la charaktérisation d'un pole, non?
Merci de me dire où est ce que je fais une erreur, et quelle est la bonne solution!
Merci beaucoup
Juste un détail pour le module, as-tu majoré le module de la somme par la somme des modules???
De plus, cos(1/z) = (exp(i/z) + exp(-i/z))/2, est tu sur que ça converge quand z tend vers 0 ?
Si on prends par exemple le suite 1/(i.n), cos(i.n) = (exp(-n) + exp(n))/2 tend vers l'infini ce qui montre que ça ne converge pas.
Le problème vient de la à mon avis et je te rappelle qu'on peux majorer le module par la différence des modules dans l'ordre qu'on souhaite mais pas par la somme. Il faut revoir le calcul de la limite.
De plus, cos(1/z) = (exp(i/z) + exp(-i/z))/2, est tu sur que ça converge quand z tend vers 0 ?
Si on prends par exemple le suite 1/(i.n), cos(i.n) = (exp(-n) + exp(n))/2 tend vers l'infini ce qui montre que ça ne converge pas.
Le problème vient de la à mon avis et je te rappelle qu'on peux majorer le module par la différence des modules dans l'ordre qu'on souhaite mais pas par la somme. Il faut revoir le calcul de la limite.
Ca na se voit pas en prépa effectivement.
Une fonction est holomorphe si elle est dérivable au sens complexe sur un domaine (ouvert connexe) D de C, c'est à dire si (f(z + h) - f(z))/h admet une limite quand h tend vers 0.
Ceci est équivalent à la différentiabilité de f en z si la différentielle est C-linéaire.
Une fonction est holomorphe si elle est dérivable au sens complexe sur un domaine (ouvert connexe) D de C, c'est à dire si (f(z + h) - f(z))/h admet une limite quand h tend vers 0.
Ceci est équivalent à la différentiabilité de f en z si la différentielle est C-linéaire.
Je suis désolé Thomas mais je ne m'y connait pas plus que toi.
Je sais juste ce qu'est une fonction holomorphe. Tout ce que j'ai dit ici venait de mes connaissance générale en calcul différentiel. Je ne sais pas ce qu'est une singularité ni un série de Laurent (bien qu'il y en avait dans le sujet de maths info de l'ENS cette année mais c'était assez facile et je me souviens plus trop)
Je sais juste ce qu'est une fonction holomorphe. Tout ce que j'ai dit ici venait de mes connaissance générale en calcul différentiel. Je ne sais pas ce qu'est une singularité ni un série de Laurent (bien qu'il y en avait dans le sujet de maths info de l'ENS cette année mais c'était assez facile et je me souviens plus trop)
J'ai fait avec la série de Laurent :
on connait le développement de cosinus, je l'ai appliqué à 1/z
un peu modifié pour pour intégre le 1/(z*z) et j'ai donc une série où l'ondexe de Sommation va jusqu'à moins l'infini. Donc un point de singularité essentiel.
(c'est ce que j'avais fait aussi dans mon premier message, mais le problème était que je pensais que ça tendait vers l'infin, donc qu'il y avait quelque chose de faux.)
Maintenant, tout va bien :)
on connait le développement de cosinus, je l'ai appliqué à 1/z
un peu modifié pour pour intégre le 1/(z*z) et j'ai donc une série où l'ondexe de Sommation va jusqu'à moins l'infini. Donc un point de singularité essentiel.
(c'est ce que j'avais fait aussi dans mon premier message, mais le problème était que je pensais que ça tendait vers l'infin, donc qu'il y avait quelque chose de faux.)
Maintenant, tout va bien :)
Si vous voulez, j'essaie de vous faire un petit résumé.
une série de Laurent, c'est une série de la forme :
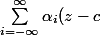^i$)
la partie de la somme de moins l'infini à -1 s'appelle Partie proncipale.
donc par exemple une fonction holomorphe (donc qui a un dévelopement en série entière) est une série de Laurent spéciale, où la partie principale est nulle.
Une série entière converge sur un disque : |z-z0| < r
Une série de Laurent converge sur une couronne : R1 < |z-z0| < R2
(R1 peut être nul, et R2 peut être infini)
Définition de singularité : z0 dans D (ouvert) est une singularité de f lorsque f est holomorphe sur D\{z0}
et le plus interessant : lorsque z0 est une singularité de f, alors on peut écrire f comme une série de Laurent, sur 0<|z-z0|<r pour un r.
Et puis ensuite on caractérise 3 types de singularités :
les fausses singularités : on peut donner une valeur pour f(z0), donc f deviendra holomorphe. La série de Laurent n'a pas de partie principale.
les poles : |f(z)| tend vers l'infini
la série de Laurent a une partie principale finie :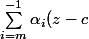^i$)
les points de singularité essentiels : la partie principale de la série de Laurent est infinie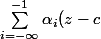^i$)
une série de Laurent, c'est une série de la forme :
la partie de la somme de moins l'infini à -1 s'appelle Partie proncipale.
donc par exemple une fonction holomorphe (donc qui a un dévelopement en série entière) est une série de Laurent spéciale, où la partie principale est nulle.
Une série entière converge sur un disque : |z-z0| < r
Une série de Laurent converge sur une couronne : R1 < |z-z0| < R2
(R1 peut être nul, et R2 peut être infini)
Définition de singularité : z0 dans D (ouvert) est une singularité de f lorsque f est holomorphe sur D\{z0}
et le plus interessant : lorsque z0 est une singularité de f, alors on peut écrire f comme une série de Laurent, sur 0<|z-z0|<r pour un r.
Et puis ensuite on caractérise 3 types de singularités :
les fausses singularités : on peut donner une valeur pour f(z0), donc f deviendra holomorphe. La série de Laurent n'a pas de partie principale.
les poles : |f(z)| tend vers l'infini
la série de Laurent a une partie principale finie :
les points de singularité essentiels : la partie principale de la série de Laurent est infinie
Salut,
ici la singularité est clairement essentielle, et comme tu l'as vu, c'est par les séries de Laurent que ce se prouve le plus facilement.
Il faut que tu te fasses confiance la dessus.
Sinon ta majoration est fausse, et j'avoue que je ne la comprend pas vraiment d'ailleurs.
En fait, par définition, pour voir si tu avais eu un pôle, tu aurais pu prendre k suffisament grand tel que z^kf(z) converge vers 0 en 0.
Ici c'est clairement impossible, donc ca n'est pas un pôle. La fonction est clairment non prolongeable par continuité en 0, tu en déduis le résultat.
En général, lorsque tu as une fonction entière g qui ne soit pas un polynôme, alors g(z) admet une singularité essentielle en l'infini.
En faisant le changement z=1/w tu as que g(w) possède une singularité essentielle en 0. Ici il est clair que cos est entière et n'est pas un polynôme, et possède donc une singularité essentielle.
L'ensemble des fonctions qui possède "au pire" des pôles, est l'ensemble des fonctions méromorphes sur C et est un corps (exercice). Autrement dit, ici tu as une fonction méromorphe + une fonction qui admet une singularité essentielle, ça ne peut être qu'une fonction qui possède une singularité essentielle.
a+
ici la singularité est clairement essentielle, et comme tu l'as vu, c'est par les séries de Laurent que ce se prouve le plus facilement.
Il faut que tu te fasses confiance la dessus.
Sinon ta majoration est fausse, et j'avoue que je ne la comprend pas vraiment d'ailleurs.
En fait, par définition, pour voir si tu avais eu un pôle, tu aurais pu prendre k suffisament grand tel que z^kf(z) converge vers 0 en 0.
Ici c'est clairement impossible, donc ca n'est pas un pôle. La fonction est clairment non prolongeable par continuité en 0, tu en déduis le résultat.
En général, lorsque tu as une fonction entière g qui ne soit pas un polynôme, alors g(z) admet une singularité essentielle en l'infini.
En faisant le changement z=1/w tu as que g(w) possède une singularité essentielle en 0. Ici il est clair que cos est entière et n'est pas un polynôme, et possède donc une singularité essentielle.
L'ensemble des fonctions qui possède "au pire" des pôles, est l'ensemble des fonctions méromorphes sur C et est un corps (exercice). Autrement dit, ici tu as une fonction méromorphe + une fonction qui admet une singularité essentielle, ça ne peut être qu'une fonction qui possède une singularité essentielle.
a+
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
