Equation second degré

[vincdel]

Bonjour,

J'ai un petit problème et j'aimerais savoir si vous pouvez m'éclaircir.

On note g(x)=(3x+2)(x²+3x)-(3x+2)²

Je dois développer et ordonner et le résultat que je trouve me paraît ambiguë.

g(x)=(3x+2)(x²+3x)-(3x+2)²
g(x)=3x^3 +2x² +9x² +6x -(9x²+6x+4)
g(x)=3x^3+2x²-4

Je dois également factoriser mais là je séché..

Si quelq'un pourrait m'aider ce serait sympas svp ;)

[Peacekeeper]

Bonjour,

tu as fait une petite erreur dans le développement de (3x+2)², relis.

Ensuite, pour factoriser (3x+2)(x²+3x)-(3x+2)² tu dois repérer les facteurs communs, n'en vois-tu pas? :happy3:

[Shew]

Bonjour,

J'ai un petit problème et j'aimerais savoir si vous pouvez m'éclaircir.

On note g(x)=(3x+2)(x²+3x)-(3x+2)²

Je dois développer et ordonner et le résultat que je trouve me paraît ambiguë.

g(x)=(3x+2)(x²+3x)-(3x+2)²
g(x)=3x^3 +2x² +9x² +6x -(9x²+6x+4)
g(x)=3x^3+2x²-4

Je dois également factoriser mais là je séché..

Si quelq'un pourrait m'aider ce serait sympas svp

Dans le cas de g(x)=(3x+2)(x²+3x)-(3x+2)² il y'a au moin un facteur commun pour chaque expression

[vincdel]

Effectivement (3x+2)² = 9x²+12x+4 me donnerais plutôt, donc si je reprend

g(x)=(3x+2)(x²+3x)-(3x+2)²
g(x)=3x^3 +2x² +9x² +6x -9x² -12x -4
g(x)=3x^3 +2x² -6x -4
Est ce bien ça ?

Pour factoriser ça devrais ressembler à
(3x+2)(x²+3x)-(3x+2)(3x+2)
Donc je prend (3x+2) en facteur commun, mais ensuite ?

[vincdel]

Effectivement (3x+2)² = 9x²+12x+4 me donnerais plutôt, donc si je reprend

g(x)=(3x+2)(x²+3x)-(3x+2)²
g(x)=3x^3 +2x² +9x² +6x -9x² -12x -4
g(x)=3x^3 +2x² -6x -4
Est ce bien ça ?

Pour factoriser ça devrais ressembler à
(3x+2)(x²+3x)-(3x+2)(3x+2)
Donc je prend 3x en facteur commun, mais ensuite ?

[Peacekeeper]

Oui, c'est ça.

Donc si tu mets 3x+2 en facteur qu'est-ce que ça te donne? Quelque chose du type (3x+2)*[...-...]

[Shew]

Effectivement (3x+2)² = 9x²+12x+4 me donnerais plutôt, donc si je reprend

g(x)=(3x+2)(x²+3x)-(3x+2)²
g(x)=3x^3 +2x² +9x² +6x -9x² -12x -4
g(x)=3x^3 +2x² -6x -4
Est ce bien ça ?

Pour factoriser ça devrais ressembler à
(3x+2)(x²+3x)-(3x+2)(3x+2)
Donc je prend 3x en facteur commun, mais ensuite ?

Seulement 3x ? Pourquoi ?

[vincdel]

En nommant (3x+2) comme facteur commun j’obtiens :
(3x+2)*[(x²+3x)-(3x+2)]
(3x+2)*[x²+3x-3x+2]
(3x+2)*[x²+2]
(3x+2)(x²+2)

Non ?

[Shew]

En nommant (3x+2) comme facteur commun j’obtiens :
(3x+2)*[(x²+3x)-(3x+2)]
(3x+2)*[x²+3x-3x+2]
(3x+2)*[x²+2]
(3x+2)(x²+2)

Non ?

Attention aux signes une fois que vous enlevez les parentheses

[vincdel]

Oh bah que je suis bête ^^

En tout cas merci bien à vous 2 ;)

[Shew]

Oh bah que je suis bête ^^

En tout cas merci bien à vous 2

Attendez c'est pas fini , postez votre réponse j'ai d'autres choses a vous reveler

[vincdel]

Ah bon, la factorisation n'est pas finie là ?
(3x+2)*[(x²+3x)-(3x+2)]
(3x+2)*[x²+3x-3x-2]
(3x+2)*[x²-2]
(3x+2)(x²-2)

[Shew]

Ah bon, la factorisation n'est pas finie là ?
(3x+2)*[(x²+3x)-(3x+2)]
(3x+2)*[x²+3x-3x-2]
(3x+2)*[x²-2]
(3x+2)(x²-2)

C'est bon mais regardez , n'y a t'il pas d'identitée remarquable qui vous saute aux yeux ?

[vincdel]

Hmm je ne vois pas là avec trois termes différents..

[Shew]

Hmm je ne vois pas là avec trois termes différents..

Cela vous rappelle t'il quelque chose ?

[vincdel]

Ah non je n'ai peut être pas encore vu ça dans le programme

[Shew]

Ah non je n'ai peut être pas encore vu ça dans le programme

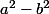
troisieme identitée remarquable .