Exercice sur les suites

[Narcisse_]

Bonjour!

J'aurais de nouveau besoin d'un tout petit coup de pouce pour la question d'un exercice :s
Voilà l'exercice :

On considère la suite (wn) dont les termes vérifient wn = [(n+1) * wn-1 + 1] / n
w0 = 1
On a obtenu le tableau suivant :
w0 w1 w2 w3 w4 w5 w6 w7 w8
1 3 5 7 9 11 13 15 17

a) Détaillez le calcul de w9 (celle-ci je l'ai faite)

b) Donner la nature de la suite (wn)

Je ne sais pas si je dois simplement dire que c'est une suite arithmétique de raison 2 ou si je dois justifier. Une amie m'a dit qu'il fallait justifier par récurrence, car quand je fais wn-1 - wn je trouve 1/(n+1) ce qui va à l'encontre de ce que je voudrais montrer..

Voilà, merci d'avance à ceux qui auront pris la peine de lire!

[Peacekeeper]

Bonsoir,

Bien sûr cela doit être démontré, mais j'avoue ne pas comprendre la méthode que tu as utilisée pour ce faire.
Tu n'ignores pas qu'une suite arithmétique est définie par la relation de récurrence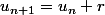 , r étant la raison de la suite.
Il te suffit donc de prouver une relation de ce type par récurrence. :happy3:

[Narcisse_]

Hmmm oui, en fait on nous a expliqué qu'il y avait une méthode pour savoir si une suite était arithmétique, c'était de faire Un+1 - Un, & si elle était arithmétique on devrait trouver 2, après je ne sais pas si elle peut ne pas marcher pour certaines suites :o

Par contre je viens de comprendre la récurrence, merci :)

[Peacekeeper]

Hmmm oui, en fait on nous a expliqué qu'il y avait une méthode pour savoir si une suite était arithmétique, c'était de faire Un+1 - Un, & si elle était arithmétique on devrait trouver 2, après je ne sais pas si elle peut ne pas marcher pour certaines suites

Par contre je viens de comprendre la récurrence, merci

Oui, cette méthode marche mais attention! On ne trouve 2 que si la raison de la suite est 2. En réalité on trouve la raison de la suite. C'est ce que je te proposais de faire en fait. Et la récurrence sert à montrer que cette relation est valable pour tous les termes de la suite.

[Narcisse_]

la raison ne serait alors pas 2? Je ne suis pas sûre d'avoir compris, j'étais déjà partie pour démontrer par récurrence que Wn = 1 + 2n (forme Un = U0 + nr) :S

[Peacekeeper]

la raison ne serait alors pas 2? Je ne suis pas sûre d'avoir compris, j'étais déjà partie pour démontrer par récurrence que Wn = 1 + 2n (forme Un = U0 + nr) :S

Si si, dans cet exercice il se trouve que la raison est 2. Ce que je voulais dire c'est que si tu dois réutiliser cette méthode sur un autre exo ne t'attends pas à retrouver 2 forcément. :happy3:

[Narcisse_]

Aaah d'accord! Oui c'était moi qui m'étais mal exprimée pardon :) Merci beaucoup!

[Peacekeeper]

Pas de quoi, bonne soirée. :happy3: