Integrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hasnaefachtab
- Membre Relatif
- Messages: 107
- Enregistré le: 07 Juil 2006, 13:05
-
 par hasnaefachtab » 07 Juil 2006, 16:22
par hasnaefachtab » 07 Juil 2006, 16:22
Bonjour,
Soit l'integrale de 0 à 1 x^n (1-x)^(1/2) dx
par une integration par parties , trouver une relation de recurrence entre In et I(n-1).
Esce (n+1)/(2n+1) In-1???
merci
-
hasnaefachtab
- Membre Relatif
- Messages: 107
- Enregistré le: 07 Juil 2006, 13:05
-
 par hasnaefachtab » 07 Juil 2006, 16:54
par hasnaefachtab » 07 Juil 2006, 16:54
up up up up up
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 07 Juil 2006, 17:45
par Sdec25 » 07 Juil 2006, 17:45
J'ai trouvé

-
hasnaefachtab
- Membre Relatif
- Messages: 107
- Enregistré le: 07 Juil 2006, 13:05
-
 par hasnaefachtab » 07 Juil 2006, 17:51
par hasnaefachtab » 07 Juil 2006, 17:51
comment?? comment??
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 07 Juil 2006, 18:04
par Sdec25 » 07 Juil 2006, 18:04

On intègre par partie :

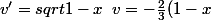^{3/2})
donc
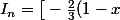^{3/2} x^n \big ]_0^1 \; - \; \int_0^1 {-\frac{2n} 3 (1-x) sqrt(1-x) x^{n-1} }dx = \frac{2n} 3 \int_0^1 { (1-x) sqrt(1-x) x^{n-1} }dx = \frac{2n} 3 (I_{n-1} - I_n))
Ensuite on sort In et on trouve la relation entre les 2.
-
hasnaefachtab
- Membre Relatif
- Messages: 107
- Enregistré le: 07 Juil 2006, 13:05
-
 par hasnaefachtab » 07 Juil 2006, 23:53
par hasnaefachtab » 07 Juil 2006, 23:53
pourquoi avez vous decider d'integrer la racine et non pas la puissance??
C'est un choix qu'on doit toujours faire???
Comment avez vous obtenu 2n/3 (In-1 - In) ???
merci
-
Thomas G
- Membre Naturel
- Messages: 55
- Enregistré le: 07 Juil 2006, 17:56
-
 par Thomas G » 07 Juil 2006, 23:58
par Thomas G » 07 Juil 2006, 23:58
Pourquoi faire tel ou tel choix ?
C'est surtout une question de feeling...
Tu en essayes un et si ça marche pas alors c'est l'autre.
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 08 Juil 2006, 00:03
par Sdec25 » 08 Juil 2006, 00:03
J'ai dérivé la puissance pour obtenir
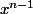
et trouver In en fonction de I(n-1).
 sqrt(1-x) x^{n-1} }dx =<br />\frac{2n} 3 \int_0^1 \big ( \sqrt{(1-x)} x^{n-1} - x \sqrt(1-x) x^{n-1} \big) dx = \frac{2n} 3 \big( \int_0^1 \sqrt{(1-x)} x^{n-1} dx -\int_0^1 \sqrt(1-x) x^{n} dx \big) = \frac{2n} 3 (I_{n-1} - I_n))
-
hasnaefachtab
- Membre Relatif
- Messages: 107
- Enregistré le: 07 Juil 2006, 13:05
-
 par hasnaefachtab » 08 Juil 2006, 00:14
par hasnaefachtab » 08 Juil 2006, 00:14
c'est un peu ambigu mais je me debrouillerai dans le concours
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
