Perdue dans les calculs de mon DM !
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Teemo
- Messages: 5
- Enregistré le: 15 Sep 2012, 18:36
-
 par Teemo » 15 Sep 2012, 18:43
par Teemo » 15 Sep 2012, 18:43
Bonjour à tous ! :zen:
Je me traine depuis 3 bonnes heures sur mon DM, et je n'arrive pas au bout !
Voilàa le sujet :
La suite (Un) est définie pour tout entier naturel n non nul par 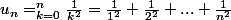 1- Demontrer que la suite Un est croissante
1- Demontrer que la suite Un est croissante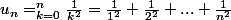
^2})
^2} >0)
Donc la suite Un est croissante
2- Démontrer par récurrence que pour tout entier naturel n non nul 
On suppose que

pour un entier n quelconque
Montrons alors que

or
^2} +u_n)
^2} +u_n \leq \frac{1}{(n-1)^2} + 2 - \frac{1}{n})
Et là je bloque !
3- Que peut on en déduire pour le comportement de la suite (Un) en 
?
Justifier.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 18:45
par Luc » 15 Sep 2012, 18:45
Bonjour!
Quelle est la question?
-
Teemo
- Messages: 5
- Enregistré le: 15 Sep 2012, 18:36
-
 par Teemo » 15 Sep 2012, 18:48
par Teemo » 15 Sep 2012, 18:48
Désolé, je m'étais trompé de bouton entre envoyer et prévisualiser, le sujet est au complet ! :) Je vais tenter de compléter avec ce que j'ai déja "trouvé"
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 15 Sep 2012, 19:05
par Luc » 15 Sep 2012, 19:05
Teemo a écrit:Désolé, je m'étais trompé de bouton entre envoyer et prévisualiser, le sujet est au complet !

Je vais tenter de compléter avec ce que j'ai déja "trouvé"
En tout cas c'est très bien écrit, félicitations!
Pour la question 2, tu as oublié l'initialisation, toujours facile à vérifier.
Ensuite, il suffit de montrer que
^2}-\frac{1}{n} \leq \frac{-1}{n+1})
-
Teemo
- Messages: 5
- Enregistré le: 15 Sep 2012, 18:36
-
 par Teemo » 15 Sep 2012, 21:10
par Teemo » 15 Sep 2012, 21:10
Haoui, pas de problème pour l'initialisation, c'est sans soucis !
Par contre je ne vois pas bien à quoi correspond ton calcul :hein: Et je suis incapable de le résoudre, j'ai beau le tourner dans tous les sens, diviser, multiplier, croiser, mixer, inverser, je n'ai rien qui me semble utile au final... Le mieux que j'ai fais c'est d'arriver à :
^2})
, et je n'ai pas l'impression que ça m'avance

-
Smileydu37
- Membre Naturel
- Messages: 10
- Enregistré le: 15 Sep 2012, 20:09
-
 par Smileydu37 » 15 Sep 2012, 21:13
par Smileydu37 » 15 Sep 2012, 21:13
Bonjours à tous, je suis en seconde et dans un exercice on me demande:
Dans un repère orthonormé du plan, tracer le cercle de centre E(3;2) passant par A(5;-1)
1- Calculer le rayon du cercle (déjà fait)
2-On considère un point M(0;y) Montrer que EM(au carré)=y(au carré)-4y+13.
3-En déduire les points d'intersection du cercle avec l'axe des ordonnées.
J'avoue que je bloque un peu pour la 2 et la 3 AIDERRRRRR MOIIIIIIII §§
Merci d'avance !
-
Teemo
- Messages: 5
- Enregistré le: 15 Sep 2012, 18:36
-
 par Teemo » 16 Sep 2012, 15:24
par Teemo » 16 Sep 2012, 15:24
Je suis toujours bloqué :'(
-
Teemo
- Messages: 5
- Enregistré le: 15 Sep 2012, 18:36
-
 par Teemo » 18 Sep 2012, 19:30
par Teemo » 18 Sep 2012, 19:30
up... je suis encore bloqué..
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 18 Sep 2012, 19:40
par Kikoo <3 Bieber » 18 Sep 2012, 19:40
Il te faut démontrer

pour tout n entier naturel non nul.
Initialisation faite ? Ok.
Hérédité. Supposons que

soit vraie à un certain n supérieur au rang initial.
Montrons qu'au rang n+1, nous avons

Or nous avons
^2})
D'après l'hypothèse de récurrence, on peut poser l'inégalité
^2}\leq ...)
.
Montrons que ce qui se trouve dans les pointillés est inférieur à

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
