Moyenne arithmético-géométrique

[Cephal]

Bonjour à tous!

On considère deux réels strictement positifs tels que aSoient (an) et (bn) deux suites définies par a0=a, b0=b et:

a(n+1)=(an+bn)/2 et b(n+1)=racine(a(n+1)bn)

- Il faut montrer que ((bn)²-(an)²) est une suite géométrique de raison 1/4.
Pour cette question, je n'ai pas eu de problèmes
- Ensuite prouver que les deux suites (an) et (bn) sont adjacentes.
Cette question me pose problème, je n'ai pas réussi à justifier la croissance de l'une et la décroissance de l'autre car le fait qu'elles soient imbriquées rend la tâche plus difficile et puis je ne vois pas comment faire pour prouver que la différence de ces deux suites tend vers 0.

[Cephal]

J'ai réussi non sans mal à justifier le fait qu'elles soient adjacentes. Maintenant, on me demande de démontrer que:

pour tout entier n non nul, bn= b*produit(cos(alpha/(2^k)), k allant de o à n) avec alpha=arccos(a/b).

J'ai réussi (vérifié à la calculatrice) que c'est égal à (a/2^n)*(sin(alpha)/sin(alpha/(2^n+1))).
J'arrive pas à lier ce truc à bn, je tourne en rond, il faut croire que cette question n'est pas démontrable :marteau: . Dans mon grand désespoir, j'offre 10 000 dollars à celui qui trouve :mur: .

[Pythales]

J'ai réussi non sans mal à justifier le fait qu'elles soient adjacentes. Maintenant, on me demande de démontrer que:

pour tout entier n non nul, bn= b*produit(cos(alpha/(2^k)), k allant de o à n) avec alpha=arccos(a/b).

J'ai réussi (vérifié à la calculatrice) que c'est égal à (a/2^n)*(sin(alpha)/sin(alpha/(2^n+1))).
J'arrive pas à lier ce truc à bn, je tourne en rond, il faut croire que cette question n'est pas démontrable :marteau: . Dans mon grand désespoir, j'offre 10 000 dollars à celui qui trouve :mur: .

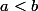
Puisque pose d'où et
etc...

garde la monnaie ...

[Cephal]

Merci beaucoup pour ton aide!!!