Devoir Maison Mathématiques, 1ère ES

[noela60]

Voilà mon exercice :

[FONT=Arial]Cette calculatrice est bizarre. Elle ne possède que deux touches A et B. L'écran, lui, n'affiche que des nombres entiers. Lorsqu'on l'allume, 0 s'affiche.
•En pressant sur la touche A, le nombre affiché est multiplié par 2, puis 1 est ajouté ;
•En pressant sur la touche B, il ne se produit quelque chose que si le nombre affiché est impair : la calculatrice lui ajoute alors 5 et divise le résultat par 2.
Vous allumez cette calculatrice. Comment obtenir l'affichage du nombre 100 en un minimum de pressions ?[/FONT]

[messinmaisoui]

Hello noela60
Je partirai du résultat ... donc de 100

[messinmaisoui]

Je reviens sur le pb de noela60 qui me reste en mémoire
comme un épine dans le pied :dodo:

y a t'il quelqu'un dans l'aimable assistance qui m'indiquerait
comment de "manière judicieuse" on pourrait procéder
pour résoudre ce pb car à part tâtonner je ne vois pas
comment faire, à la reflexion ?

De mon coté j'aurais sans doute écrit un programme
récursif traitant toutes les possibilités en empruntant tous les
chemins possibles pour trouver la/les bons chemins s'ils existent
Bref le MERLIN pour enfoncer une pointe ... :doh:

[cachender]

Il faut arriver à 100, moi j'aurais opter aussi de partir du chiffre 100 mais comme tu dit je le ferai à taton.
En regardant il faut peut etre partir du départ quand même
On à 0 on appuie sur A on obtient 1 apresè que l'on appuye sur A ou B ca change rien on obtiendra toujours 3 et à partir de la on continu pour a mon avis arriver à 195 et finir en apuuyant sur B à partir de 195 on en déduit qu'on avait avant appuyer sur A et donc qu'on avait 97... etc je vais y réfléchir un peu j'espère avoir pu aider

[cachender]

J'ai trouver une solution en 13 coups

[messinmaisoui]

Merci cachender

La question est de savoir si il n'y a pas une solution < 13 coups :lol3:
Sans démonstration comment en être certain ?

[p-convexe]

Hello noela60
Je partirai du résultat ... donc de 100

Bonjour,
C'est la bonne idée, il me semble.
Je ne crois pas que ce qui suit soit très rigoureux !
La dernière touche doit donner 100, il faut donc que ce soit B, car si c'était A on devrait avoir 2k+1=100 c'est impossible k serait fractionnaire. Plus généralement l'appui sur la touche A ne peut fournir qu'un nombre impair.
Le nombre précédent 100 doit être 195, car la touche B donne : (195 +5)/2 = 100
Voyons ce qui est le plus rapide, appuyer sur A ou B ?
Soit le nombre k :
- touche A : 2k+1
- touche B : (k+5)/2
comparons : 2k+1 ? (k+5)/2 --> 4k+2 ? k+5 --> 3k ? 3 --> k ? 1 ==> la touche A accroit plus vite la "montée" vers 100, sauf si k=1 (A ou B fournissent le même résultat).
Donc je vais appuyer sur A tant que je le peux, sinon je presserais B.
Notons que la 1ère touche doit être A , car B ne donne rien (de plus la calculatrice fonctionne logiquement puique 0 est pair !).
Voici la suite que l'on obtient [notation ci-dessous : k(A) signifie que on a appuyé sur A pour obtenir k, idem si k(B) : on a appuyé sur B]
100(B) 195(A) 97(A) 48(A) 91(B , A est impossible car 48 est pair) 45(A) 22(A) 39(B) 19(A) 9(A) 4(A) 3(B) . 3 peut s'obtenir en pressant A ou B.
Donc il faut 14 pressage de touches.
Si tout cela est bon , la démonstration est "besogneuse"ne me semble pas du tout élégante

Cordialement.

[messinmaisoui]

Merci bien p-convexe !!

"besogneuse" peut-être ... mais expliquée et bien commentée

Par contre cachender a trouvé 13 coups ... à vérifier si ça n'est pas 14 au final
ou alors en partant de 0 vers 100 ...

en tout cas Merci à vous 2

[p-convexe]

Merci bien p-convexe !!

"besogneuse" peut-être ... mais expliquée et bien commentée

Par contre cachender a trouvé 13 coups ... à vérifier si ça n'est pas 14 au final
ou alors en partant de 0 vers 100 ...

en tout cas Merci à vous 2

J'ai mal compté ! Ma série est de 13 coups (et non 14 , j'avais compté 2 fois 3(B).

[Frednight]

Considérons cette calculatrice. Celle-ci applique une fonction ou une fonction au nombre qu'elle a en mémoire selon le bouton sur lequel on appuie.

On note par exemple que prend n'importe quel entier, le transforme dans un premier temps en un entier obligatoirement pair (puisque pouvant s'écrire sous la forme de où en réalité 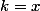) pour ensuite en faire un nombre impair en lui ajoutant . On a ainsi :


De la même manière, prend, elle, un nombre impair, le transforme en nombre pair en lui ajoutant un nombre impair qui est (la somme deux nombres impairs 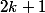et donne , nombre divisible par , donc pair) et finit en le divisant par deux : on arrive ainsi avec un nombre entier quelconque. On a ainsi :


Considérons à présent les fonctions et 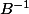respectivement réciproques de et , i.e. fonctions telles que et . En gros, on cherche des fonctions telles que, en prenant par exemple , si ajoute à un nombre, alors sa fonction réciproque soustraira 4 de sorte que cela fasse comme si on ne les avait jamais utilisées. cela revient à faire le chemin en sens inverse.
Concrètement, pour , on a d'abord multiplié par puis on a ensuite ajouté au résultat obtenu. doit donc d'abord permettre d'"effacer" cette addition du en le soustrayant à puis d'ensuite occulter la multiplication par en divisant le tout par ce même chiffre. On tient en outre compte du fait que l'on part cette fois-ci d'un nombre impair pour arriver à un entier quelconque. Concrètement cela donne :

De la même façon pour :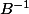


Connaître l'expression de ces deux fonctions permet alors, comme suggéré dans les messages précédents, de partir de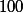 pour arriver à sans tâtonner.

Partons de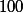 , nombre pair. On ne peut alors appliquer que la fonction : la calculatrice affiche alors . 1 pression de bouton.

est impair : on applique donc la fonction . La calculette affiche alors . 2 pressions

Ainsi de suite cela fait alors :


On trouve ainsi 13 pressions de bouton nécessaires, seul moyen d'arriver selon moi à 100 en partant de 0.

[Frednight]

Je corrige ce que j'ai dit plus haut : ce n'est pas le seul moyen d'y arriver. On peut en effet appliquer autant de fois que l'on veut mais cela fait croître notre suite de valeurs au lieu de l'amener à 0. Il faut donc l'employer le moins de fois possibles (soit uniquement lorsque l'on ne peut utiliser parce que est pair).

[chan79]

J'ai mal compté ! Ma série est de 13 coups (et non 14 , j'avais compté 2 fois 3(B).

13 coups pour moi aussi
A - A - B - A - A - A - B -A - A - B - A - A - B
1 -3- 4- 9-19-39-22-45-91-48-97-195-100
mais on peut remplacer le second A, à partir de la gauche, par B, ça revient au même puisque:
1*2+1=3 et (1+5)/2=3

[messinmaisoui]

Purée, en 1ere le niveau a sérieusement évolué !

[Frednight]

Purée, en 1ere le niveau a sérieusement évolué !

j'ai hyper formalisé ma solution mais avec un peu de logique on peut en venir à bout je pense...

[p-convexe]

(Re)Bonjour,

J'ai raisonné autrement:
Je pars toujours de 195 (on ne peut y échapper). Pour trouver la touche précédente , je considère les 2k+1 et (k+5)/2 divisant 195, ... etc pour les touches précédentes.
En s'intéressant à la parité de k [par exemple, si k = 2k'+1] on simplifie l'expression analytique des nombres précédents. je ne sais pas ce que ça peut donner , car j'étais devant la télévision, mais il y a peut-être une solution pour moins de 10 touches (?!)

Cordialement.

p-convexe

[chan79]

(Re)Bonjour,

J'ai raisonné autrement:
Je pars toujours de 195 (on ne peut y échapper). Pour trouver la touche précédente , je considère les 2k+1 et (k+5)/2 divisant 195, ... etc pour les touches précédentes.
En s'intéressant à la parité de k [par exemple, si k = 2k'+1] on simplifie l'expression analytique des nombres précédents. je ne sais pas ce que ça peut donner , car j'étais devant la télévision, mais il y a peut-être une solution pour moins de 10 touches (?!)

Cordialement.

p-convexe

Une petite moulinette permet d'envisager rapidement toutes les possibilités en 13 coups. Aucune ne fait arriver à 100 à moins de 13 coups, sauf erreur

[Frednight]

(Re)Bonjour,

J'ai raisonné autrement:
Je pars toujours de 195 (on ne peut y échapper). Pour trouver la touche précédente , je considère les 2k+1 et (k+5)/2 divisant 195, ... etc pour les touches précédentes.
En s'intéressant à la parité de k [par exemple, si k = 2k'+1] on simplifie l'expression analytique des nombres précédents. je ne sais pas ce que ça peut donner , car j'étais devant la télévision, mais il y a peut-être une solution pour moins de 10 touches (?!)

Cordialement.

p-convexe

Non on ne peut pas le faire en moins de 13 pressions. Toujours pour en revenir à mon explication, considérons les deux fonctions réciproques et . On part de et on veut arriver à en un minimum de pressions. Il faut donc que chaque pression fasse baisser la valeur du nombre affiché par la calculette au maximum.
En reprenant ce que l'on a marqué précédemment, on a :


Si fait baisser la valeur , cela équivaut à :

Donc fera baisser la valeur de tout naturel pour peu que celui-ci soit impair (elle n'accepte pas les entiers pairs).
Pour , cela donne :

Donc n'est vraiment avantageux que lorsque est inférieur à (comme l'a fait remarquer Chan). En revanche, il est tout de même utile (même s'il fait augmenter notre nombre au lieu de le diminuer lorsque ce nombre est supérieur à ) puisqu'il transforme obligatoirement un naturel quelconque en un nombre impair, nombre impair que pourra transformer la fonction .
Cela donne alors :


il faut donc veiller à utiliser le plus de fois possible la fonction , ce que nous avons fait dans les exemples précédents et qui donne 13 pressions.

[p-convexe]

Bonjour,
Donc on ne peut pas réussir en moins de 13 coups, c'est bien établi.
Cependant il manque une démonstration rigoureuse de cela, dommage !
---
Au fait, le prof. (s'il y en a un) qui a posé le problème a peut-être la démonstration ?

Cordialement.

p-convexe

[chan79]

on veut arriver à en un minimum de pressions. Il faut donc que chaque pression fasse baisser la valeur du nombre affiché par la calculette au maximum.

Pas évident ... il pourrait monter pour mieux redescendre
Je ne vois qu'un test de tous les cas ( soit 8192 façons) mais sans ordinateur ... ?
Mais une vraie démonstration existe peut-être ...

[noela60]

merci beaucoup de votre aide, à tous, mais j'ai finalement trouvé la solution tout seul ! Et après vérification avec vos réponses, il s'est avéré que j'avais juste. Merci en tout cas pour votre aide :)))))))))