Justification : quel théorème?

[Aud39]

Bonjour, je comprends bien la preuve suivante mais de quel théorème général s'agit-il SVP?

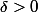
On considère n'importe quel pour lequel est différenciable. On pose . Ainsi :



et de façon similaire :

.

Et grâce à ces deux inégalités on obtient que .


Je pensais à la définition d'une fonction dérivable pour les limites (avec lim à gauche et lim à droite qui sont égales) mais la formule dans mes cours n'est pas tout à fait la même...

Merci.

[Luc]

Salut,

le théorème général (ou plutôt la définition)est le suivant :
Vu les notations, j'imagine que u est une fonction d'une variable réelle.
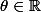
Soit . On dit que est dérivable en si le taux d'accroissement admet une limite lorsque . On appelle cette limite le nombre dérivé de en .

[Aud39]

Salut,

le théorème général (ou plutôt la définition)est le suivant :
Vu les notations, j'imagine que u est une fonction d'une variable réelle.
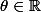
Soit . On dit que est dérivable en si le taux d'accroissement admet une limite lorsque . On appelle cette limite le nombre dérivé de en .

Ah et bien c'est bien à ce que je pensais alors... Merci !

[Luc]

Ah et bien c'est bien à ce que je pensais alors... Merci !

Attention à la généralisation pour une fonction de plusieurs variables car la notion de différentiabilité est plus forte que la dérivabilité pour une variable. En effet, il existe des fonctions qui admettent des dérivées partielles dans toutes les directions mais qui ne sont pas différentiables (même pas continues).
En revanche, l'existence ET la continuité des dérivées partielles entraine l'existence de la différentielle en un point, et même un peu mieux.

[Aud39]

Attention à la généralisation pour une fonction de plusieurs variables car la notion de différentiabilité est plus forte que la dérivabilité pour une variable. En effet, il existe des fonctions qui admettent des dérivées partielles dans toutes les directions mais qui ne sont pas différentiables (même pas continues).
En revanche, l'existence ET la continuité des dérivées partielles entraine l'existence de la différentielle en un point, et même un peu mieux.

Très bien, merci pour cette précision.

J'avais un doute sur la définition (u est bien une fonction d'une variable réelle, ) car ce que j'ai retrouvé dans mon cours est :

f est dérivable en si le taux d'accroissement entre et admet une limite quand x tend vers , i.e. si :


existe.


Or dans l'exemple on a qui tend vers 0 et comme est au dénominateur je pensais que du coup dans ce cas la fraction tendait vers l'infini...