Seconde - Fraction - Irréductible
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
smrh2002
- Membre Naturel
- Messages: 32
- Enregistré le: 09 Sep 2009, 17:38
-
 par smrh2002 » 09 Sep 2012, 19:39
par smrh2002 » 09 Sep 2012, 19:39
Bonjour
Démontrer quelque soit n la fraction suivante est irréductible :
} {(n+1)})
Voilà ce que j'ai commencé à faire puis je reste bloqué:
}{n+1} = \frac{n^2} {n+1} + 3)
Merci pour votre aide
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 09 Sep 2012, 20:53
par Iroh » 09 Sep 2012, 20:53
Salut, tu peux aussi observer que
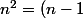(n+1)+1)
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 09 Sep 2012, 21:00
par SaintAmand » 09 Sep 2012, 21:00
Iroh a écrit:Salut, tu peux aussi observer que
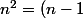(n+1)+1)
Ou aussi regarder ce qui se passe si un nombre premier divise n² et n+1.
-
smrh2002
- Membre Naturel
- Messages: 32
- Enregistré le: 09 Sep 2009, 17:38
-
 par smrh2002 » 10 Sep 2012, 06:51
par smrh2002 » 10 Sep 2012, 06:51
Bonjour
SaintAmand a écrit:Ou aussi regarder ce qui se passe si un nombre premier divise n² et n+1.
Merci à vous deux mais je ne vois toujours pas comment continuer.
Iroh : avec ton aide j'ai
+\frac{1}{n+1}+3)
. Je pense calculer après le PGCD de
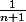
qui me donne 1.
Saint Amand : Je ne vois pas comment s'y prendre ... Tu pourras me donner uns petite explication supplémentaire. Nombre premier : nombre divise par 1 et lui même .. Faut il que je calcule le PGCD de

et n+1 ?
Merci
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 10 Sep 2012, 07:55
par Iroh » 10 Sep 2012, 07:55
Je ne sais pas quelle méthode tu utilises en classe pour savoir si une fraction est irréductible, mais tu obtiens là une somme de 2 fractions irréductibles

(dont le pgcd de chacune vaut 1), et quand tu les mets au même dénominateur (ppcm des deux dénom.), tu obtiens la fraction initiale, qui est donc irréductible.
Sinon une méthode pour calculer le pgcd entre deux nombre qui utilise la division euclidienne. Tu dois d'abord montrer que

pour tout

.
 Source: http://www.playermath.com
Source: http://www.playermath.com

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Sep 2012, 07:55
par chan79 » 10 Sep 2012, 07:55
smrh2002 a écrit:Bonjour
Merci à vous deux mais je ne vois toujours pas comment continuer.
Iroh : avec ton aide j'ai
+\frac{1}{n+1}+3)
. Je pense calculer après le PGCD de
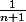
qui me donne 1.
Saint Amand : Je ne vois pas comment s'y prendre ... Tu pourras me donner uns petite explication supplémentaire. Nombre premier : nombre divise par 1 et lui même .. Faut il que je calcule le PGCD de

et n+1 ?
Merci
Slt
n²+3n+3=n²+3(n+1)
Soit d un diviseur commun à (n²+3n+3) et à (n+1)
D'après l'égalité ci-dessus, d divise n² et (n+1)
S'il y avait un nombre premier dans la décomposition de d, il diviserait n et (n+1) ce qui est impossible car deux entiers consécutifs sont premiers entre eux.
donc d=1 et l'expression proposée est irréductible

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Sep 2012, 08:06
par chan79 » 10 Sep 2012, 08:06
ou sinon
l'égalité n²-(n+1)(n-1)=1 montre que n² et (n+1) sont toujours premiers entre eux
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 10 Sep 2012, 20:14
par SaintAmand » 10 Sep 2012, 20:14
Iroh a écrit:Je ne sais pas quelle méthode tu utilises en classe pour savoir si une fraction est irréductible, mais tu obtiens là une somme de 2 fractions irréductibles

(dont le pgcd de chacune vaut 1), et quand tu les mets au même dénominateur, tu obtiens la fraction initiale, qui est donc irréductible.
Je n'arrive pas à identifier quelle propriété tu utilises pour justifier que la somme des 2 fractions irréductibles est une fraction irréductible.
-
smrh2002
- Membre Naturel
- Messages: 32
- Enregistré le: 09 Sep 2009, 17:38
-
 par smrh2002 » 11 Sep 2012, 09:13
par smrh2002 » 11 Sep 2012, 09:13
Merci pour toutes vos réponses. Pour moi il y a toujours une zone d'ombre. Mais je vais creuser un peu plus les différentes explications.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités

. Je pense calculer après le PGCD de
qui me donne 1.
et n+1 ?
(dont le pgcd de chacune vaut 1), et quand tu les mets au même dénominateur, tu obtiens la fraction initiale, qui est donc irréductible.