Salut,
la partie entière E est nulle puisque le degré de la fraction rationnelle est strictement négatif.
Ensuite, tu es sur la bonne voie. Il y a cinq inconnues scalaires, il faut donc cinq équations linéaires indépendantes. Inutile donc de se précipiter pour faire les calculs tant que tu n'en as pas cinq.
La méthode des pôles que tu as utilisée pour b et e est très bien.
Ensuite, il faut prendre trois valeurs particulières de x, de préférence simples.
Il y a pour cela une astuce facultative mais bien pratique : multiplier par x et évaluer en l'infini.
Ça donne
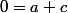
.
La valeur en

donne

comme tu l'as dit.
La valeur en
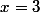
donne

.
En remplaçant b et e par leur valeur et en remplaçant c par -a, on obtient un système linéaire de deux équations à deux inconnues pour a et d.

,

d'où l'on tire a=-8 et d=-6.
Finalement,
^2 (x-2)^3})
=
} - \frac{2}{(x-1)^2} + \frac{8}{(x-2)} - \frac{6}{(x-2)^2} + \frac{4}{(x-2)^3})
