Re : Intégration par partie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
juve305
- Membre Naturel
- Messages: 17
- Enregistré le: 28 Aoû 2012, 12:25
-
 par juve305 » 02 Sep 2012, 16:57
par juve305 » 02 Sep 2012, 16:57
Re bonsoir,
Est-ce que cette intégration est correcte :
.dx)
g' = x² => g=
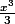
f = ln(x) =>

= ln(x).
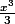
-

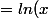.\frac{x^3}{3} - \frac{1}{3} \bigint_{.}^{.} \frac{x^3}{3}.dx)
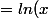.\frac{x^3}{3} - \frac{1}{3} \bigint_{.}^{.} x^2.dx)
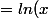.\frac{x^3}{3}-\frac{1}{3}.\frac{x^3}{3}+k)
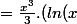-\frac{1}{3})+k)
Merci

-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 02 Sep 2012, 17:07
par Luc » 02 Sep 2012, 17:07
Salut,
juve305 a écrit:Re bonsoir,
Est-ce que cette intégration est correcte :
.dx)
g' = x² => g=
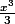
f = ln(x) =>

= ln(x).
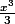
-

Ok.
juve305 a écrit: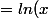.\frac{x^3}{3} - \frac{1}{3} \bigint_{.}^{.} \frac{x^3}{3}.dx)
Non. (faute de frappe?)
juve305 a écrit: 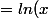.\frac{x^3}{3} - \frac{1}{3} \bigint_{.}^{.} x^2.dx)
Oui.
juve305 a écrit: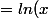.\frac{x^3}{3}-\frac{1}{3}.\frac{x^3}{3}+k)
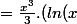-\frac{1}{3})+k)
C'est correct (tu peux vérifier en dérivant le résultat).
Ce calcul s'appelle une primitivation plutôt qu'une intégration (lintégration c'est avec des bornes).
Exercice : Généralise le résultat a une fonction du type P(x)ln(x) ou P est une fonction polynomiale.
Luc
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 08 Sep 2012, 08:31
par geegee » 08 Sep 2012, 08:31
Bonjour,
En intégrant par partie:
u(x)=ln(x) u'(x)=1/x
v'(x)=x^2 v(x)=x^3/3
integrale de (x^2.ln(x))=[ln(x).x^3/3]-x^3/9+k=ln(x).x^3/3-x^3/9+k= x^3/3(ln(x)-1/3)+k (k dans R)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
.dx)

-
