Hyperplan d'appui dans un espace de Banach ?

[acoustica]

Bonjour aux insomniaques,

Je me posons une question relative à la notion d'hyperplan d'appui. Elle a été définie dans mon cours dans le cadre des espaces de Hilbert, ce qui a un sens puisque faisant appel aux produits scalaires et servant à démontrer le théorème de séparation d'un point et d'un convexe. Néanmoins je me demandais s'il y avait un sens à définir un hyperplan d'appui dans un espace de Banach, c'est-à-dire sans munir l'espace d'un produit scalaire. Intuitivement, je serais tenté de penser que le produit scalaire n'est qu'un outil pour démontrer le théorème de séparation, mais qu'on pourrait s'en délester en utilisant d'autres astuces, par exemple en ne raisonnant qu'avec des distances.
Est-ce un problème de dimension : finie ou infinie ?

Merci d'avance et bonne soirée !

[Arkhnor]

C'est moi qui rêve, ou les messages de cette discussion ont été supprimés ?

J'avais posté deux messages, et acoustica un autre, et ils n'apparaissent plus. :hum:

EDIT : La réponse ici. Les messages ont certainement été perdus lors de la migration du serveur.

[Sylviel]

Il n'y à aucun message supprimé dans cette discussion (que je puisse voir). Donc si c'est le cas c'est un problème technique :hum:

Sinon oui il est parfaitement possible de parler d'hyperplan d'appui dans un Banach, il suffit de pouvoir parler de son dual. (Sous réserve)

[Arkhnor]

Visiblement, si l'on lit le topic de Tom_Pascal, il est possible que des messages aient été perdus pendant la migration du serveur.

Donc, dans mon premier message, je disais que c'est le théorème de séparation de Hahn-Banach (la version géométrique) qui assure l'existence d'un hyperplan d'appui. La page wiki pour plus d'infos : http://fr.wikipedia.org/wiki/S%C3%A9paration_des_convexes

J'ajoutais alors que l'existence d'un hyperplan d'appui ne nécessite donc pas de produit scalaire (qui rend le théorème de Hahn-Banach presque trivial), et donc est assurée dans un espace normé, et même dans un evt localement convexe.

Suite à la dernière remarque, acoustica me demandait alors la signification d'evt localement convexe.

Ma réponse :

EVT = Espace Vectoriel Topologique; c'est-à-dire un espace vectoriel muni d'une topologie qui rend continue l'addition et la multiplication par les scalaires.

C'est le cas de la topologie d'un espace normé. De même, si au lieu d'avoir une seule norme, on a une famille de semi-normes, on peut aussi associer naturellement une topologie d'evt. Ce qui nous amène logiquement à la seconde notion :

EVT localement convexe = EVT dont la topologie est celle associée à une famille de semi-normes.

Le nom vient du fait suivant : un evt est localement convexe si et seulement si 0 possède une base de voisinages convexes.

La version géométrique du théorème de Hahn-Banach est vraie pour les evt localement convexes.
La majorité (pour ne pas dire la totalité) des evts intéressants sont localement convexes.

[Tom_Pascal]

Bonjour,

Je suis désolé Arkhnor, c'est effectivement dû à un problème technique dû à une migration de serveur, faite dans des conditions un peu particulières... Plus d'informations ici.

Quelques messages ont pu être perdus, nous avons fait le maximum pour que la migration soit rapide, mais bon ...

[Arkhnor]

Sinon oui il est parfaitement possible de parler d'hyperplan d'appui dans un Banach, il suffit de pouvoir parler de son dual. (Sous réserve)

Effectivement, en parler, on peut toujours. Le plus délicat est surtout de prouver qu'il en existe au moins un.

[Arkhnor]

Tom_Pascal, pas de problème, j'avais encore le souvenir de mes réponses.
(et ravi de te voir aussi ici, on ne peut qu'espérer le mieux pour Maths-Forum dans l'avenir)

[acoustica]

Visiblement, si l'on lit le topic de Tom_Pascal, il est possible que des messages aient été perdus pendant la migration du serveur.

Donc, dans mon premier message, je disais que c'est le théorème de séparation de Hahn-Banach (la version géométrique) qui assure l'existence d'un hyperplan d'appui. La page wiki pour plus d'infos : http://fr.wikipedia.org/wiki/S%C3%A9paration_des_convexes

J'ajoutais alors que l'existence d'un hyperplan d'appui ne nécessite donc pas de produit scalaire (qui rend le théorème de Hahn-Banach presque trivial), et donc est assurée dans un espace normé, et même dans un evt localement convexe.

Suite à la dernière remarque, acoustica me demandait alors la signification d'evt localement convexe.

Ma réponse :

EVT = Espace Vectoriel Topologique; c'est-à-dire un espace vectoriel muni d'une topologie qui rend continue l'addition et la multiplication par les scalaires.

C'est le cas de la topologie d'un espace normé. De même, si au lieu d'avoir une seule norme, on a une famille de semi-normes, on peut aussi associer naturellement une topologie d'evt. Ce qui nous amène logiquement à la seconde notion :

EVT localement convexe = EVT dont la topologie est celle associée à une famille de semi-normes.

Le nom vient du fait suivant : un evt est localement convexe si et seulement si 0 possède une base de voisinages convexes.

La version géométrique du théorème de Hahn-Banach est vraie pour les evt localement convexes.
La majorité (pour ne pas dire la totalité) des evts intéressants sont localement convexes.

Super Arkhnor, merci beaucoup à toi pour toutes ces précisions. Tu anticipes même ma deuxième interrogation, sur le sens des semi-normes. Ca s'éclaircit bien. =)

[Arkhnor]

Juste un mot sur comment on définit la topologie associée à une famille de semi-normes.

Si on a un espace vectoriel , muni d'une famille de semi-normes, alors pour chaque semi-norme, on a les boules ouvertes associées.
On dit alors que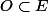 est ouvert si et seulement si pour tout 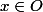, il existe 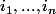dans et 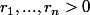des rayons tels que .

Comme chaque boule pour une semi-norme est convexe, et que l'intersection de convexes est convexe, on voit que 0 possède une base de voisinages convexes.
C'est la réciproque (prouver que si 0 possède une base de voisinages convexes, alors la topologie est définie par des semi-normes) qui est plus délicate : ça passe par les jauges de Minkowski.

[acoustica]

Juste un mot sur comment on définit la topologie associée à une famille de semi-normes.

Si on a un espace vectoriel , muni d'une famille de semi-normes, alors pour chaque semi-norme, on a les boules ouvertes associées.
On dit alors que est ouvert si et seulement si pour tout , il existe dans et des rayons tels que .

Comme chaque boule pour une semi-norme est convexe, et que l'intersection de convexes est convexe, on voit que 0 possède une base de voisinages convexes.
C'est la réciproque (prouver que si 0 possède une base de voisinages convexes, alors la topologie est définie par des semi-normes) qui est plus délicate : ça passe par les jauges de Minkowski.

Dac... Mais pourquoi le définir avec de semi-normes et non des normes ? En quoi l'uni-direction, la demi-droite et non la droite est-elle importante ?

[Arkhnor]

Je ne comprends pas ce que tu veux dire lorsque tu parles de demi-droite ou d'uni-direction.
Je rappelle qu'une semi-norme c'est la même chose qu'une norme, exceptée qu'on a perdu la propriété : la semi-norme d'un vecteur peut-être 0 sans que le vecteur soit nul.

En particulier, toute norme est une semi-norme, et la construction de topologies à l'aide de semi-normes est plus générale que celle avec des normes.

Si tu te restreins uniquement aux topologies associées à des familles de normes, tu perds beaucoup d'exemples intéressants.

Un parmi beaucoup d'autres : supposons qu'on veuille munir de la convergence uniforme sur tout compact.

(la convergence uniforme sur tout entier est généralement beaucoup trop forte pour les applications, et de plus ce n'est pas une topologie d'evt : 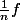ne tend pas vers 0 si n'est pas bornée)

Dire qu'une suite de fonctions converge uniformément sur tout compact vers signifie que pour tout compact 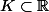, on a .
On est donc naturellement amené à introduire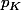 définie par : converge uniformément sur tout compact vers signifie alors que pour tout compact .

Les applications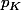 sont seulement des semi-normes, et non des normes : implique seulement que est nulle sur .

PS : Impossible de visualiser le LaTeX pour l'instant; la migration n'aime pas beaucoup cette discussion. :ptdr:

[Tom_Pascal]

PS : Impossible de visualiser le LaTeX pour l'instant; la migration n'aime pas beaucoup cette discussion.

Yep, je suis un peu pénible :chaise: ... je cherche à corriger un bug mais j'avais temporairement cassé le LaTeX.

Encore désolé.