Merci de votre aide
Déduction
21 messages
- Page 1 sur 2 - 1, 2
par capitaine nuggets » 30 Aoû 2012, 16:22
Bonjour,
Développe ce produit, puis montre que(y+z)(z+x)=(y^2+z^2)x+(x^2+z^2)y+(x^2+y^2)z+2xyz)
.
déduis-en le résultat :++:
alphanom a écrit:Bonjour, je dois désuire de cette inégalité :,
celle ci :,
Merci
Développe ce produit, puis montre que
déduis-en le résultat :++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
par chan79 » 31 Aoû 2012, 16:32
Océane9170 a écrit:Apres ? je ne vois pas ou en venir avec cette valeur absolue (Je n'ai presque pas abordé ce chapitre)
tu ajoutes membre à membre puis tu ajoutes de chaque côté 2xyz
par Kikoo <3 Bieber » 01 Sep 2012, 09:38
Océane9170 a écrit:Connais pas IAG >__< ... C'est 'Inégalité Arithmético-Géométrique (IAG)'v mais je connais pas x) ...
exact,
Nous avons
En réappliquant ceci sur chaque facteur le résultat vient naturellement.
par Kikoo <3 Bieber » 01 Sep 2012, 09:58
Non pas sur la forme réduite mais sur celle du début, qui est un produit de facteurs :
(x+y)(y+z)(x+z)
Mais cette méthode est trop puissante et rapide.
edit : au fait il est donné comme condition que x, y et z sont réels positifs.
Cette contrainte favorise l'utilisation de l'IAG
(x+y)(y+z)(x+z)
Mais cette méthode est trop puissante et rapide.
edit : au fait il est donné comme condition que x, y et z sont réels positifs.
Cette contrainte favorise l'utilisation de l'IAG
par Kikoo <3 Bieber » 01 Sep 2012, 10:30
Bon et bien il faut expliquer plusieurs choses :
L'inégalité Arithmético-Géométrique (IAG) est formulée comme ceci :
Soit une liste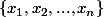
de n termes indicés positifs.
Nous avons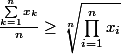
Le cas où n=2 est facile à montrer :
Soient a et b deux réels positifs.
Nous avons toujours :^2\geq 0)
Ainsi
d'où immédiatement : 
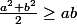
Si nous considérons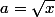
, 
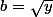, il vient :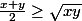 
Pour en revenir à ce cas-ci, nous avons :
\in\mathbb{R}^*^3)
d'où :
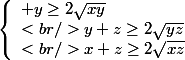
En multipliant terme à terme le résultat en découle :
(y+z)(x+z)\geq 2\times 2\times 2\times \sqrt{x^2\times y^2\times z^2}=8xyz)
L'inégalité Arithmético-Géométrique (IAG) est formulée comme ceci :
Soit une liste
Nous avons
Le cas où n=2 est facile à montrer :
Soient a et b deux réels positifs.
Nous avons toujours :
Ainsi
Si nous considérons
Pour en revenir à ce cas-ci, nous avons :
En multipliant terme à terme le résultat en découle :
par Kikoo <3 Bieber » 01 Sep 2012, 10:47
Pour la méthode Chan-CptNuggets, nous avons :
(y+z)(x+z) \\<br />=(xy+xz+y^2+yz)(x+z) \\<br />=x^2y+x^2z+xy^2+xyz+xyz+xz^2+zy^2+yz^2 \\<br />=x(y^2+z^2)+y(x^2+z^2)+z(x^2+y^2)+2xyz)
Et là on utilise l'IAG (toujours elle) pour remarquer que :
x \geq 2xyz \\<br />(x^2+z^2)y \geq 2xyz \\<br />(x^2+y^2)z \geq 2xyz)
On ajoute membre à membre, comme le suggère Chan :
+y(x^2+z^2)+z(x^2+y^2)\geq 6xyz)
et on rajoute
:
+y(x^2+z^2)+z(x^2+y^2)+2xyz=(x+y)(y+z)(x+z)\geq 8xyz)
Et là on utilise l'IAG (toujours elle) pour remarquer que :
On ajoute membre à membre, comme le suggère Chan :
et on rajoute
par Kikoo <3 Bieber » 01 Sep 2012, 11:51
Océane9170 a écrit:Merci pour toutes ces explications qui m'ont permis de voir enfin la lumiere x) ..
Avec plaisir
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :