Problème avec les degrés
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Littlemathy
- Membre Naturel
- Messages: 11
- Enregistré le: 29 Aoû 2012, 17:40
-
 par Littlemathy » 30 Aoû 2012, 16:04
par Littlemathy » 30 Aoû 2012, 16:04
Voilà,
(pour ceux qui auraient lu mon précédent post) après la division euclidienne (par moments) je bloque sur les degrés... Je n'arrive absolument pas à comprendre comment on peut trouver la réponse à ces calculs, mais je pense surtout qu'il y a de la théorie que je ne connais pas et que je n'ai visiblement pas! :triste:
Je vous mets un exemple de mon cours:
1)

La réponse du 1) serait:

En fait je ne sais pas d'où sort le 1? On le déduit, on choisit, c'est de la théorie? :look2:
Merci de vos réponses!

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2012, 16:09
par ampholyte » 30 Aoû 2012, 16:09
Littlemathy a écrit:Voilà,
(pour ceux qui auraient lu mon précédent post) après la division euclidienne (par moments) je bloque sur les degrés... Je n'arrive absolument pas à comprendre comment on peut trouver la réponse à ces calculs, mais je pense surtout qu'il y a de la théorie que je ne connais pas et que je n'ai visiblement pas! :triste:
Je vous mets un exemple de mon cours:
1)

La réponse du 1) serait:

En fait je ne sais pas d'où sort le 1? On le déduit, on choisit, c'est de la théorie? :look2:
Merci de vos réponses!
Bonjour,
Je m'en sors pas avec les balises donc je te conseille de faire un petit tour ici :
http://uuu.enseirb.fr/~gloess/enseignement/ateliers/2004_2005/student_projects/belfkih_bousraou_daou/J'imagine qu'en jouant avec les binomiales il est possible de trouver la réponse à ta question.
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 30 Aoû 2012, 16:17
par Billball » 30 Aoû 2012, 16:17
a0, a1, a2 ... correspondent bien au coefficient des différents degré en x ??
comment ça peut valoir 1 ? sachant que 2^12 fait déja 4096

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2012, 16:18
par ampholyte » 30 Aoû 2012, 16:18
Billball a écrit:a0, a1, a2 ... correspondent bien au coefficient des différents degré en x ??
comment ça peut valoir 1 ? sachant que 2^12 fait déja 4098
C'est possible vu que c'est -2 donc tu as aussi 3*(-2)^11 = -6144,
Ainsi les termes vont se compenser au fur et à mesure.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Aoû 2012, 16:23
par chan79 » 30 Aoû 2012, 16:23
Littlemathy a écrit:Voilà,
(pour ceux qui auraient lu mon précédent post) après la division euclidienne (par moments) je bloque sur les degrés... Je n'arrive absolument pas à comprendre comment on peut trouver la réponse à ces calculs, mais je pense surtout qu'il y a de la théorie que je ne connais pas et que je n'ai visiblement pas! :triste:
Je vous mets un exemple de mon cours:
1)

La réponse du 1) serait:

En fait je ne sais pas d'où sort le 1? On le déduit, on choisit, c'est de la théorie? :look2:
Merci de vos réponses!
slt=
P(1)=(3*1-2)^12=(3-2)^12=1^12=1

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2012, 16:25
par ampholyte » 30 Aoû 2012, 16:25
chan79 a écrit:slt2=
P(1)=(3*1-2)^12=(3-2)^12=1^12=1
Je pense que la question était plutôt d'où sortait le P(1) ^^ ou plutôt pourquoi la somme des termes serait égale à P(1).
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 30 Aoû 2012, 16:25
par Billball » 30 Aoû 2012, 16:25
exact, je trouve 1 également
-
Littlemathy
- Membre Naturel
- Messages: 11
- Enregistré le: 29 Aoû 2012, 17:40
-
 par Littlemathy » 30 Aoû 2012, 16:30
par Littlemathy » 30 Aoû 2012, 16:30
ampholyte a écrit:Je pense que la question était plutôt d'où sortait le P(1) ^^ ou plutôt pourquoi la somme des termes serait égale à P(1).
Oui tout à fait!

:hein:

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2012, 16:32
par ampholyte » 30 Aoû 2012, 16:32
Littlemathy a écrit:Oui tout à fait!

:hein:
As-tu vu la formule du binôme de Newton ?
-
Littlemathy
- Membre Naturel
- Messages: 11
- Enregistré le: 29 Aoû 2012, 17:40
-
 par Littlemathy » 30 Aoû 2012, 16:41
par Littlemathy » 30 Aoû 2012, 16:41
Non, désolé :triste: :hum:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Aoû 2012, 16:50
par Carpate » 30 Aoû 2012, 16:50
Littlemathy a écrit:Non, désolé :triste: :hum:
Si tu remplaces x par 1 dans l'expression de P(x), tu obtiens

qui est la somme des coeff. de P(x) et qui vaut P(1) lequel vaut
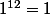

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2012, 17:03
par ampholyte » 30 Aoû 2012, 17:03
Carpate a écrit:Si tu remplaces x par 1 dans l'expression de P(x), tu obtiens

qui est la somme des coeff. de P(x) et qui vaut P(1) lequel vaut
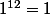
:mur:, si évident pourtant.
Calculer la somme S revient à calculer P(1). S = P(1).
J'étais parti très loin (à la recherche d'une formule généralisant la valeur de la somme en fonction de x)
-
C.Ret
- Membre Relatif
- Messages: 497
- Enregistré le: 02 Juil 2012, 12:33
-
 par C.Ret » 30 Aoû 2012, 18:09
par C.Ret » 30 Aoû 2012, 18:09
Et oui, il y a parfois des énoncés qui semblent compliqués alors qu'ils utilisent une astuce très simple !
C'est le type de sujet que j'aime poser aux oraux, il permet de voir si le candidat sait garder la tête froide en toute circonstance et ne pas paniquer ou stresser.
Un polynôme de degré 12 peut faire peur (à première vue). Remarquons que le problème se résous de la même manière avec un polynôme de degré 120, 2345 ou 45678. Mais en utilisant de degré aussi élevé, le piège marche moins bien; on met la puce à l'oreille du candidat.
Inversement, j'ai eut des résolutions très compliquées avec des polynôme de degré 3 ou 4. En général, 75% des candidats développent le polynôme, calculent tous les coefficients a_i pour en faire finalement la somme.
La majorité arrivent à la bonne réponse (assez vite parfois). Mais c'est bien plus compliqué que de calculer P(1) !
-
Littlemathy
- Membre Naturel
- Messages: 11
- Enregistré le: 29 Aoû 2012, 17:40
-
 par Littlemathy » 30 Aoû 2012, 18:14
par Littlemathy » 30 Aoû 2012, 18:14
Donc si je comprends bien, la somme serait P(x), mais lorsque l'on remplace x par le coefficient qui le représente? (je ne sais pas si je suis claire).
Je veux dire qu'en fait, on doit recherché ce que vaudrait x pour qu'une fois effectué, le tout vaudrait

? Et ainsi connaitre ce que vaut la somme? (si ce n'est pas cela, expliquez bieeeen en détails parce que j'ai eu déjà du mal à faire cette conclusion :hum:)
-
Littlemathy
- Membre Naturel
- Messages: 11
- Enregistré le: 29 Aoû 2012, 17:40
-
 par Littlemathy » 30 Aoû 2012, 19:06
par Littlemathy » 30 Aoû 2012, 19:06
J'ai bon, ou faux? Où c'est une manière de voir les choses?:hum:

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 30 Aoû 2012, 19:09
par ampholyte » 30 Aoû 2012, 19:09
Littlemathy a écrit:J'ai bon, ou faux? Où c'est une manière de( voir les choses?:hum:
En fait,
On te demande de calculer la somme S définit par
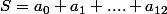
.
Pour cela, on te donne
 = (3x-2)^{12} = a_0 + a_1 x+a_2 x + ... + a_{12} x^{12})
On peut remarquer que pour x = 1 on a
 = a_0+a_1+....+a_{12})
On peut donc dire que
 = S)
.
Du coup on peut aussi écrire
 = S = (3*1-2)^{12} = 1)
.
As-tu compris ?
-
Littlemathy
- Membre Naturel
- Messages: 11
- Enregistré le: 29 Aoû 2012, 17:40
-
 par Littlemathy » 31 Aoû 2012, 09:45
par Littlemathy » 31 Aoû 2012, 09:45
Aaaaah, je vois enfin! :D Merci, j'ai compris maintenant ^_^
-
C.Ret
- Membre Relatif
- Messages: 497
- Enregistré le: 02 Juil 2012, 12:33
-
 par C.Ret » 01 Sep 2012, 10:07
par C.Ret » 01 Sep 2012, 10:07
Ah!Très bien.
Je susi désolé, je me rends compte seulement maintenant que nulle part nous avions précisisé simplement :
Quelque soit le polynôme

de degré

,
)
est la somme de ces coefficients et
)
est le coefficient

.
En effet :
Quel que soit
\,=\,a_n.x^n\,+a_{n-1}.x^{n-1}\,+a_{n-2}.x^{n-2}\,+\,...\,+a_2.x^2+a_1.x+a_0)
On a
\,=\,a_n.1^n\,+a_{n-1}.1^{n-1}\,+a_{n-2}.1^{n-2}\,+\,...\,+a_2.1^2+a_1.1+a_0\\<br />P(1)\,=\,a_n.1\;+a_{n-1}.1\;+a_{n-2}.1\;+\,...\,+a_2.1\;+a_1.1+a_0\\<br />P(1)\,=\,a_n\;+a_{n-1}\;+a_{n-2}\;+\,...\,+a_2\;+a_1\;+a_0)
Et
\,=\,a_n.0^n\,+a_{n-1}.0^{n-1}\,+a_{n-2}.0^{n-2}\,+\,...\,+a_2.0^2+a_1.0+a_0\\<br />P(0)\,=\,a_n.0\;+a_{n-1}.0\;+a_{n-2}.0\;+\,...\,+a_2.0\;+a_1.0+a_0\\<br />P(0)\,=0. \left ( a_n+a_{n-1}\,+a_{n-2}\,+\,...\,+a_2\,+a_1 \right )+a_0\\<br />P(0)\,=\,a_0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités



 ? Et ainsi connaitre ce que vaut la somme? (si ce n'est pas cela, expliquez bieeeen en détails parce que j'ai eu déjà du mal à faire cette conclusion :hum:)
? Et ainsi connaitre ce que vaut la somme? (si ce n'est pas cela, expliquez bieeeen en détails parce que j'ai eu déjà du mal à faire cette conclusion :hum:)