Limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 30 Aoû 2012, 13:48
par izoard » 30 Aoû 2012, 13:48
Bonjour,
je n'arrive à démontrer proprement que si
)
,
alors
=cste)

=0)
Merci d'avance
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 13:56
par acoustica » 30 Aoû 2012, 13:56
izoard a écrit:Bonjour,
je n'arrive à démontrer proprement que si
)
,
alors
=cste)

=0)
Merci d'avance
Bonjour,
C'est sans doute parce que c'est faux.
La fonction
}{x^2+1})
qui converge vers 0, est C1 sur R et a une dérivée qui ne converge pas vers 0.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 30 Aoû 2012, 13:58
par izoard » 30 Aoû 2012, 13:58
OK . Merci .
Et est il possible de rajouter des hypothèses sur f qui rendraient vraie l'implication que j'ai énoncée ??
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 14:01
par acoustica » 30 Aoû 2012, 14:01
izoard a écrit:OK . Merci .
Et est il possible de rajouter des hypothèses sur f qui rendraient vraie l'implication que j'ai énoncée ??
Je ne sais pas, mais par contre je connais un résultat qui s'en rapproche :
Si

, alors

.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 30 Aoû 2012, 14:01
par izoard » 30 Aoû 2012, 14:01
Peut être si f' converge . Je vais regarder de plus près
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 14:02
par acoustica » 30 Aoû 2012, 14:02
izoard a écrit:Peut être si f' converge . Je vais regarder de plus près
A oui, il y a fort à parier que si on rajoute l'hypothèse que f ' converge, et si f tend vers une constante, alors f ' converge vers 0. C'est même certain^^.
Mais je t'ai mis au-dessus un autre résultat intéressant.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 30 Aoû 2012, 14:05
par Luc » 30 Aoû 2012, 14:05
acoustica a écrit:Je ne sais pas, mais par contre je connais un résultat qui s'en rapproche :
Si

, alors

.
Oui car si f et f' convergent, alors f' converge forcément vers 0 (par Taylor-Lagrange), donc f converge vers 0 puisque f+f' converge vers 0.
Une condition plus faible serait d'avoir f' bornée? Mais ce n'est pas suffisant pour assurer que f' converge.
=\frac{sin(x^2)}{x})
tend vers 0 mais
=2cos(x^2)-\frac{sin(x^2)}{x^2})
n'admet pas de limite bien que bornée.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 30 Aoû 2012, 14:06
par chan79 » 30 Aoû 2012, 14:06
izoard a écrit:OK . Merci .
Et est il possible de rajouter des hypothèses sur f qui rendraient vraie l'implication que j'ai énoncée ??
peut-être que si f est strictement croissante... ??? à voir de près
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 14:10
par acoustica » 30 Aoû 2012, 14:10
Luc a écrit:Oui car si f et f' convergent, alors f converge forcément vers 0 (par Taylor-Lagrange).
Une condition plus faible serait d'avoir f' bornée? Mais je ne sais pas si cela est suffisant.
Mmmh, je ne suis pas convaincu. Ca reviendrait à faire la même erreur de raisonnement qui consiste à passer de f à f', mais ici en passant de f' à f'', etc... Je vais essayer de mettre en forme ton idée, mais je ne pense pas qu'on s'en sorte comme ça. Je ne me souviens plus de la démonstration de ce résultat je l'avoue. Enfin j'essaye quand même. On s'y colle ensemble ? :we:
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 30 Aoû 2012, 14:12
par Luc » 30 Aoû 2012, 14:12
acoustica a écrit:Mmmh, je ne suis pas convaincu. Ca reviendrait à faire la même erreur de raisonnement qui consiste à passer de f à f', mais ici en passant de f' à f'', etc... Je vais essayer de mettre en forme ton idée, mais je ne pense pas qu'on s'en sorte comme ça. Je ne me souviens plus de la démonstration de ce résultat je l'avoue.
Non, si tu supposes que f' converge vers

non nul, alors Taylor-Lagrange permet d'écrire que
)
est équivalent à
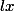
au voisinage de l'infini, ce qui est absurde. Donc f' converge vers 0.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 14:16
par acoustica » 30 Aoû 2012, 14:16
Luc a écrit:Non, si tu supposes que f' converge vers

non nul, alors Taylor-Lagrange permet d'écrire que
)
est équivalent à
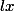
au voisinage de l'infini, ce qui est absurde. Donc f' converge vers 0.
Ah oui d'accord, mais ça c'est pour démontrer que si on rajoute l'hypothèse que f ' converge vers unee constante non nulle, alors cette constante est nulle. Mais ça c'est l'idée de izoar qui voulait rajouter une hypothèse de croissance à partir d'un certain rang (ou de décroissance). Je parlais de l'autre problème que je soulevais à la question d'avant...
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 14:16
par acoustica » 30 Aoû 2012, 14:16
Luc a écrit:Non, si tu supposes que f' converge vers

non nul, alors Taylor-Lagrange permet d'écrire que
)
est équivalent à
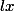
au voisinage de l'infini, ce qui est absurde. Donc f' converge vers 0.
Au temps pour moi j'ai dis des bêtises. Je m'incline. =)
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 14:18
par acoustica » 30 Aoû 2012, 14:18
Attends, mais ce comportement de f ' peut être compensé par le comportement de f. Le fait que f ' ne soit pas convergent vers 0 en l'infini peut être contrebalancé par f. Je pense qu'il faut regarder simultanément f et f '.
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 30 Aoû 2012, 14:22
par Luc » 30 Aoû 2012, 14:22
acoustica a écrit:Au temps pour moi j'ai dis des bêtises. Je m'incline. =)
Sinon je vois pas quelle hypothèse on peut faire d'autre que f' bornée.
Peut être f monotone? f convexe?
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 14:29
par acoustica » 30 Aoû 2012, 14:29
Pour lim(f+f')=0 => lim(f)=0
On cherche le comportement de g:=f+f '.
On a une équation différentielle du premier ordre :
(E0) : f+f'=0 donc f(x)=a*e^{-x}.
(a(x)exp(-x))'=a'(x)exp(-x)-a(x)exp(-x)
f+f'=a'(x)exp(-x)=g(x) qui tend vers 0.
a'(x)=g(x)*exp(x) avec a'(x)=o(exp(x))
donc f+f'=o(exp(x)*exp(-x))=o(1)
A vérifier, je crains les abus de notations.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 30 Aoû 2012, 14:35
par izoard » 30 Aoû 2012, 14:35
Luc a écrit:Non, si tu supposes que f' converge vers

non nul, alors Taylor-Lagrange permet d'écrire que
)
est équivalent à
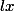
au voisinage de l'infini.
Je n'arrive pas à démontrer ça ... :mur:
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 30 Aoû 2012, 14:47
par Luc » 30 Aoû 2012, 14:47
izoard a écrit:Je n'arrive pas à démontrer ça ... :mur:
Fais le avec des

en utilisant la définition de la limite, et en utilisant l'égalité
=f(A)+\int_{A}^{x}f'(t)dt)
valable au voisinage de l'infini. Cela permet d'encadrer
}{x})
par

et

pour

assez grand, ce qui montre le résultat.
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 30 Aoû 2012, 15:10
par acoustica » 30 Aoû 2012, 15:10
Pour le problème : montrer que si

, alors

.
On cherche le comportement de g:=f+f '.
On a une équation différentielle du premier ordre :
(E0) :

donc
=a*e^{-x})
exp(-x))'=a'(x)exp(-x)-a(x)exp(-x))
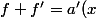exp(-x)=g(x)=o(1))
=\int_{0}^{x}{g(t)*exp{-t}}dt+C)
d'où
=\int_{0}^{x}{g(t)*exp(t-x)}dt+C*exp(-x))
avec g(x)=o(1).
g tend vers 0 donc il existe un rang A à partir duquel pour
\ge A)
, on a : g(x)<g(A)
=\int_{h(A)}^{x}{g(t)*exp(t-x)}dt+B*exp{-x} \\ \le g(A)\int_{h(A)}^{x}{exp{t-x}}dt+B*exp(-x) \\<br /><br />=g(A)exp(-x)*\int_{h(A)}^{x}{exp{t}}dt+B*exp(-x) \\<br />=g(A)exp(-x)*(exp{x}-exp{h(A)})+B*exp(-x)\\<br />=g(A)-exp(h(A))g(A)exp(-x)+B*exp{-x} \\)
qui est arbitrairement petit pour A assez grand.
Je pense qu'on pourrait aussi s'en sortir avec le lemme de Gronwall.
Démonstration à vérifier, je ne suis pas sûr du tout de mon coup.
-
izoard
- Membre Naturel
- Messages: 75
- Enregistré le: 06 Nov 2011, 18:44
-
 par izoard » 30 Aoû 2012, 15:59
par izoard » 30 Aoû 2012, 15:59
Merci à tous les deux !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
, alors
.
non nul, alors Taylor-Lagrange permet d'écrire que
est équivalent à
au voisinage de l'infini, ce qui est absurde. Donc f' converge vers 0.