Démo inégalité somme quadratique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ipon
- Messages: 6
- Enregistré le: 12 Aoû 2012, 15:44
-
 par ipon » 12 Aoû 2012, 15:57
par ipon » 12 Aoû 2012, 15:57
Bonjour a tous je me demande bien comment prouver l'inégalité suivante :
avec b>a

J'ai remarqué que l'expérience prouve cette inégalité cependant le prouver mathématiquement reste un sérieux dilemne .
Merci à tous ceux qui essaieront d'apporter une solution ^^!
-
Aurelius1212
- Membre Naturel
- Messages: 19
- Enregistré le: 16 Juil 2012, 11:07
-
 par Aurelius1212 » 12 Aoû 2012, 17:02
par Aurelius1212 » 12 Aoû 2012, 17:02
Bonjour,
b>a veut dire bi > ai quelque soit i ou bien en terme de norme ? (vecteurs)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 12 Aoû 2012, 17:11
par chan79 » 12 Aoû 2012, 17:11
ipon a écrit:Bonjour a tous je me demande bien comment prouver l'inégalité suivante :
avec b>a

J'ai remarqué que l'expérience prouve cette inégalité cependant le prouver mathématiquement reste un sérieux dilemne .
Merci à tous ceux qui essaieront d'apporter une solution ^^!
salut
essaie avec n=

-
ipon
- Messages: 6
- Enregistré le: 12 Aoû 2012, 15:44
-
 par ipon » 12 Aoû 2012, 17:27
par ipon » 12 Aoû 2012, 17:27
En fait dans mon probème j'ai oublié de préciser que a et b sont positifs et que b > a dans tout les cas peu importe le i.
-
Aurelius1212
- Membre Naturel
- Messages: 19
- Enregistré le: 16 Juil 2012, 11:07
-
 par Aurelius1212 » 12 Aoû 2012, 17:30
par Aurelius1212 » 12 Aoû 2012, 17:30
ipon a écrit:En fait dans mon probème j'ai oublié de préciser que a et b sont positifs et que b > a dans tout les cas peu importe le i.
justement il y a un problème de vocabulaire, si a =(a1,...ai,...,an) et b=(b1,...,bi,...,bn), dire que b>a ne veut rien dire du tout. Donc c'est bien bi>ai quelque soit i ?
De toute manière ta formule n'est pas vrai pour des vecteurs à une dimension.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 12 Aoû 2012, 17:58
par chan79 » 12 Aoû 2012, 17:58
ipon a écrit:Bonjour a tous je me demande bien comment prouver l'inégalité suivante :
avec b>a

J'ai remarqué que l'expérience prouve cette inégalité cependant le prouver mathématiquement reste un sérieux dilemne .
Merci à tous ceux qui essaieront d'apporter une solution ^^!
Salut
c'est bizarre
essaie avec
n=0
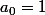
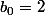
-
ipon
- Messages: 6
- Enregistré le: 12 Aoû 2012, 15:44
-
 par ipon » 13 Aoû 2012, 08:11
par ipon » 13 Aoû 2012, 08:11
Tout a fait b(i) > a(i) quel que soit i.
Ca ne semble pas fonctionner dans ton exemple en n= 0 mais apres ca a l'air de bien marché dans mon expérience ( dans la réalité n tourne entre 50 et 500).

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 13 Aoû 2012, 10:48
par chan79 » 13 Aoû 2012, 10:48
ipon a écrit:Tout a fait b(i) > a(i) quel que soit i.
Ca ne semble pas fonctionner dans ton exemple en n= 0 mais apres ca a l'air de bien marché dans mon expérience ( dans la réalité n tourne entre 50 et 500).
avec n=1

ça n'a pas l'air d'aller non plus
Peut-être qu'à partir d'un certain n, ça marche ?
-
ipon
- Messages: 6
- Enregistré le: 12 Aoû 2012, 15:44
-
 par ipon » 13 Aoû 2012, 13:11
par ipon » 13 Aoû 2012, 13:11
Il doit exister une différence entre l'équation et mon expérience. D'un autre coté en pratique, b est largement supérieur à a . Je pensais que cette équation était toujours valable mais apparement elle ne fontionne effectivement qu'a partir d'un certain rang. b est a peu pres égal à 3 voir 4 fois a. De plus, n ne peut pas non plus être inférieur à deux.
-
C.Ret
- Membre Relatif
- Messages: 497
- Enregistré le: 02 Juil 2012, 12:33
-
 par C.Ret » 13 Aoû 2012, 13:17
par C.Ret » 13 Aoû 2012, 13:17
Il faut peut-être des

et

particuliers ?
Pourquoi y-a-t-il des crochets autour de l'inégalité ?
-
ipon
- Messages: 6
- Enregistré le: 12 Aoû 2012, 15:44
-
 par ipon » 13 Aoû 2012, 13:52
par ipon » 13 Aoû 2012, 13:52
C.Ret a écrit:Il faut peut-être des

et

particuliers ?
Pourquoi y-a-t-il des crochets autour de l'inégalité ?
les crochets ne doivent pas être là. Il ne faut pas s'en occuper. Je ne connais pas réellement le domaine de variations des ai et bi. Je peux simplement donner l'ordre de grandeur cité ci dessus et affirmer que pour tout i : a(i) < b(i)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 13 Aoû 2012, 15:12
par chan79 » 13 Aoû 2012, 15:12
ipon a écrit:Il doit exister une différence entre l'équation et mon expérience.
Tu devrais préciser l'expérience correspondant à cette inégalité. On pourra peut-être t'aider un peu plus
-
ipon
- Messages: 6
- Enregistré le: 12 Aoû 2012, 15:44
-
 par ipon » 14 Aoû 2012, 08:14
par ipon » 14 Aoû 2012, 08:14
Je peux pas donner plus de détails dsl.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
et
particuliers ?