libertad a écrit:Merci pour ta réponse, mais je peux exprimer
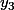
par :
}{g(y_1)} + h(y_1))
avec
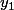
qui est fonction de

,

et
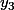
Donc là, j'ai un peu l'impression de tourner en rond ... Quelque chose doit méchapper.
Faut il que je considère une des variables comme fixe ?
Au début, tu commences par parler d'une variable n puis elle disparaît dans tes précisions dans les posts suivants.
A certains endroits, il me semble que tu confonds variable et fonction ...
Alors, quelle est vraiment ton problème ?
*****
y3 = f(x1,x3)/g(x1,x2,x3) + h(x1,x2,x3)
Je suppose :
- que x1, x2 et x3 sont des variables indépendantes les unes des autres ... (sinon quelle sont les fonctions qui les relient)
- que f est une fonction connue des variables x1 et x3
- que g et h sont des fonctions connues des variables x1, x2 et x3
- Et que donc y2 est aussi une fonction des variables x1, x2 et x3
Si c'est bien cela ... Quelle est la question ?
Et si ce n'est pas cela, alors qu'est-ce ?
*****
?
