Théorème du graphe fermé

[egan]

Salut tout le monde,

Je dispose de l'énoncé suivant:

Soit E et F deux espaces de Banach et T une application linéaire de E dans F.
Si le graphe de T:



est fermé, alors T est continue.

Ma question est la suivante:

Quelle norme on met sur E x F ?
Je mettrais bien .

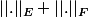
Merci d'avance.
@+ Boris.

[girdav]

Oui, n'importe quel norme qui donne la topologie produit (des topologies données par les normes).

[egan]

Je suis un peu perdu là. Ca veut dire que toutes les normes sont équivalentes ?

Qu'est-ce que tu appelles une norme qui donne la topologie produit ? La topologie est définie par la norme normalement non ?

[girdav]

Si tu prend une norme sur , alors la norme va convenir.

Dans ce contexte, graphe fermé signifie graphe fermé dans la topologie produit. Comme on aime bien travailler avec des suites pour vérifier qu'un graphe est fermé, il faut trouver une norme qui correspond à la topologie produit (en fait une distance suffirait, mais vu que l'on a déjà des normes, on peut prendre une norme). Les normes de la forme ci-dessus conviennent, mais toutes les normes sur l'espace produit (non nécessairement de cette forme) ne sont pas équivalentes pour peu que l'un des espaces soit de dimension infinie.

[egan]

Donc le théorème est vrai avec toute norme sur E x F ?

Qu'est-ce la topologie produit ? Elle est pas censée être définie par la norme que l'on met sur E x F ?

[girdav]

Normalement, si tu travailles le théorème du graphe fermé, tu travailles l'analyse fonctionnelle et tu as du faire de la topologie. Dans ce cas, tu as vu que la topologie produit est la topologie la moins fine qui contient tous les pavés ouverts, et en exercice on montre que c'est la même que la topologie donnée par la norme que tu indiques.

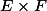
Je ne comprends pas ce que tu veux dire par "toute norme sur " : on pourrait probablement imaginer un cas pervers où l'on prend une norme qui ne donne pas la topologie produit, et que le graphe serait fermé pour cette norme mais pas pour la topologie produit.

[egan]

Ah ok. Je n'ai pas vu ça.
J'ai fait la topo de MP* mais là je suis en école d'ingé et je n'ai fait pas ça.
Effectivement, je m'intéresse à l'analyse fonctionnelle en ce moment.

Si on reprend un peu. Corrige moi si je dis une bêtise.

La topologie, c'est l'ensemble des ouverts.
Une topologie dépend donc d'une norme.
Une topologie A est moins fine qu'une topologie B si B est inclus dans A.

Tu as dit que:

La topologie produit est la topologie la moins fine qui contient tous les pavés ouverts.

Ce serait pas plutôt:

La topologie produit est la topologie la moins fine qui contient tous les pavés d'ouverts.

Donc d'une manière générale, quand on doit mettre une norme sur un produit, on met la norme que j'ai proposé ?

[girdav]

La norme que tu as proposée convient en effet.

En revanche, ce n'est pas vrai que toute topologie dépend d'une norme. Le fait qu'il est une une norme suppose que l'on a une structure d'espace vectoriel, ce n'est pas supposé dans un espace topologique quelconque. De plus, il y a des topologies, même séparés, qui ne sont induites par aucune distance.

Qu'est-ce que tu entends par "pavés d'ouverts" ?

[egan]

Pour pavé d'ouverts, je pensais à: A x B, avec A et B des ouverts.

[girdav]

Moi aussi, donc c'est ok :)

[egan]

J'ai besoin du théorème du graphe fermé pour les Banach moi. Je voulais essayer de le montrer mais je suis bloqué.

Je munis ExF de la norme que j'avais proposé.
On remarque tout d'abord que ExF est alors un Banach.
En plus de ça, ((e_n;f_n)) est de Cauchy dans ExF si et seulement si (e_n) l'est dans E et (f_n) l'est dans F.

Je suppose le graphe de f fermé. f est linéaire donc si je montre qu'elle est continue en 0, c'est fini. Je me donne donc une suite de E (x_n) qui converge vers 0. Je veux alors montrer que (f(x_n)) converge vers 0.

J'ai le sentiment qu'il faut réussir à montrer que (x_n;f(x_n)) est de Cauchy. Alors elle converge vers (x;y). x vaut forcément 0 et comme le graphe de f est fermé, y vaut f(0)=0. Et la démo est finie.

Problème: comment montrer que (x_n;f(x_n)) est de Cauchy ? Il est clair que le problème revient à montrer que (f(x_n)) est de Cauchy. Mais comment faire cela ?

[girdav]

Je crois qu'il n'y a pas le choix et qu'il faut utiliser un "gros " théorème, dans le sens que serait long de tout faire à la main. On définit sur la norme du graphe , et le fait que le graphe soit fermé assure que muni de cette norme est aussi un espace de Banach. Puis on invoque le théorème d'isomorphisme de Banach.