Inéquation du 2nd degré

[Coco13]

Bonjour,

La solution de l'inéquation est : x(x+6)>-5
La résolution de l'inéquation du second degré est : x(car) + 6x + 5>0
Le premier membre est un trinôme du second degré de racines (apparentes) -1 et -5.

Ma question est la suivante : comment déterminer les racines apparentes ?
Par ailleurs, comment savoir que le trinôme est positif (du signe de son coefficient a) pour les valeurs extérieures à l'intervalle des racines ?

Par avance merci.

[vincentroumezy]

Bonjour.
Qu'appelles tu "racines apparentes" ?
Pour déterminer les racines dun polynômes du second degré, tu utilises la formule, vue en cours, qui utilise le discriminant.

[C.Ret]

Autre solution, mais moins évidente à mon sens: comme on donne les deux racines x1 et x2, on factorise par et .

Dans notre cas:






D'où les deux racines "apparentes"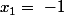 et

Concernant le signe du polynôme entre et en-dehors de l'intervalle défini par ses racines, je ne me souviens jamais de la règle. Je fais donc un essais en prenant une valeur de test soit entre les racine, soit en dehors.

[Coco13]

Merci,

Néanmoins, avec et sans le discriminant, l'évidence mentionnée dans le corrigé de l'exercice, des racines -1 et -5 m'échappe totalement.

[Black Jack]

Merci,

Néanmoins, avec et sans le discriminant, l'évidence mentionnée dans le corrigé de l'exercice, des racines -1 et -5 m'échappe totalement.

x(x+6)>-5

x² + 6x + 5 > 0
x² + 6x + 9 - 4 > 0
(x+3)² - 4 > 0
(x+3)² - 2² > 0
(x+3-2)(x+3+2) > 0
(x+1)(x+5) > 0

Tableau de signes ...

Solutions: x dans ]-oo ; -5[ U ]-1 ; +oo[

:zen:

[Mortelune]

Il arrive de parler de racines évidentes d'un polynôme lorsque -1, 0 ou 1 sont racines, peut être aussi parfois pour -2 et 2 parce que ce sont des valeurs qui peuvent se tester "facilement" - de tête. Et on sait que si on connait une racine r d'un polynôme il peut se factoriser par (x-r) donc si -1 est racine on factorise par (x+1) et comme le polynôme est du second degré il reste à trouver a, l'autre racine du polynôme et on a ici que -1*a=5 donc a=-5. S'il y avait eu un coefficient différent de 1 devant x² il aurait aussi fallu factoriser par ce coefficient et aménager la dernière étape. Enfin cette technique repose pour l'essentiel sur une volonté de raccourcir la rédaction, si on n'est pas à l'aise avec ça utiliser une solution plus méthodique n'est pas à exclure.

[C.Ret]

x(x+6)>-5

x² + 6x + 5 > 0
x² + 6x + 9 - 4 > 0
(x+3)² - 4 > 0
(x+3)² - 2² > 0
(x+3-2)(x+3+2) > 0
(x+1)(x+5) > 0

Tableau de signes ...

Ca faisait longtemps :

Code: Tout sélectionner

         | -oo            -5                -1            +oo
---------+----------------------------------------------------
 (x+5)   |       -         0       +         +        +
         |                                 
 (x+1)   |       -         -       -         0        +     
         |                                 
---------+----------------------------------------------------
x(x+6)+5 |       +         0       -         0        +
---------+----------------------------------------------------   
d'où     |                 :                 :
x(x+6)   |  x(x+6)>-5     =-5   x(x+6)-5


Solutions: x dans ]-oo ; -5[ U ]-1 ; +oo[

:zen:

[Coco13]

Merci,

Finalement j'ai pu le résoudre avec le discriminant, sans factoriser de façon aussi talentueuse !