Calcul de limites

[Deluxor]

Bonsoir,

Je travaille des annales de concours, et voici des limites que j'ai à calculer. Pouvez-vous me donner quelques pistes, et/ou me corriger?



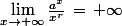
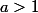
1) Montrer que : pour et .

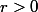
2) Déterminer

3) ?


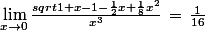
Merci d'avance!

[savancosinus]

Bonjour,

La 3) je suis d'accord avec toi
La 2) tu peux te ramener à des termes de la forme qui se simplifieront.

Par contre pour la 1) c'est un résultat de cours (croissance comparée des puissances et des exposants), soit on te demande juste la réponse en disant que c'est un résultat de cours, soit on te demande de le redémontrer, et là il y a le cours pour t'aider.

[Deluxor]

Merci de ta réponse savancosinus !

J'ai redémontré la 1).

Pour la 2), je ne vois pas comment simplifier... J'essayais :



Mais bon... ^^

Pour la 3), ok!

[savancosinus]

Non ça ne va pas beaucoup t'aider ça.

Essaie de faire apparaître des termes de la forme
ensuite par des équivalences lorsque ça va se simplifier tout seul.

[Deluxor]

C'est bien ça?

[savancosinus]

Salut,

Ta première ligne est correcte, la seconde non.
Tu te trompes dans tes équivalents, tu ne peux pas te retrouver avec du

EDIT. Enfin si tu peux toujours mais ça ne t'aidera pas. Il faut travailler avec les équivalents classiques du cours.

[savancosinus]

Salut,

Ta première ligne est correcte, la seconde non.
Tu te trompes dans tes équivalents, tu ne peux pas te retrouver avec du

EDIT.
Enfin si tu peux toujours, mais ça ne t'aidera pas. il faut utiliser les équivalents classiques du cours.