Bonjour,
J 'ai un exercice d'analyse pour lequel j'avais pensé avoir une super idée,
Après réflexion, je me demande si ce n'est pas un bluff grossier complètement
faux comme dirait mon prof.
L'énoncé est simple : f une fonction continue sur [0,+infini[ qui admet une
limite L quand x -> +infini. Montrer que f est uniformément continue sur
[0, +infini[.
Alors je pense qu'en revenant à la def d'une limite en +infini, on pourrait se débrouiller
mais voilà ce que je propose :
f admet une limite en +infini donc on considère g, son prolongement continue
sur "R barre +", ie g:[0,+infini] -> R
Or "R barre +" est un compact donc par Heine, g est uniformément
continue ainsi que sa restriction à R+ qui est f.
Bon déja "R barre + est un compact", je n'en suis pas sûr, on nous a juste dit
que R barre en est un (je suis en MP), je suppose donc que "R barre +"
en est un aussi, mais, d'une façon générale je ne saisis pas trop en quoi R barre
est un fermé borné.
Bonus : Pouvez vous me citer un fermé non borné "usuel" , je ne vois pas trop.
Et pour finir mon raisonnement est-il correct ?
Merci de m'éclairer !
Un peu de TOPO..
6 messages
- Page 1 sur 1
Salut, je ne pense pas que ta démo marche telle quelle. En effet, 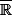 est compact, mais pour appliquer Heine il faut le munir d'une structure d'espace métrique. C'est possible, mais les distances sur
est compact, mais pour appliquer Heine il faut le munir d'une structure d'espace métrique. C'est possible, mais les distances sur 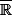 (genre d'(x,y) = |th(x) - th(y)|) ne sont pas des extensions de la distance usuelle sur
(genre d'(x,y) = |th(x) - th(y)|) ne sont pas des extensions de la distance usuelle sur  . Y a peut-être encore un moyen de s'en sortir et de passer de la continuité uniforme sur
. Y a peut-être encore un moyen de s'en sortir et de passer de la continuité uniforme sur ) à la continuité uniforme sur
à la continuité uniforme sur ) , mais faudra le justifier et c'est pas la démarche attendue à mon avis.
, mais faudra le justifier et c'est pas la démarche attendue à mon avis.
Reste dans et passe par les définitions epsilonesques. Si x et y sont suffisamment grands, tu peux utiliser la définition de la limite. Sinon, tu peux enfermer x et y dans un segment et utiliser l'uniforme continuité de f sur ce segment. Ça demande deux-trois manips mais ça doit marcher.
et passe par les définitions epsilonesques. Si x et y sont suffisamment grands, tu peux utiliser la définition de la limite. Sinon, tu peux enfermer x et y dans un segment et utiliser l'uniforme continuité de f sur ce segment. Ça demande deux-trois manips mais ça doit marcher.
Reste dans
Skullkid a écrit:Salut, je ne pense pas que ta démo marche telle quelle. En effet,est compact, mais pour appliquer Heine il faut le munir d'une structure d'espace métrique. C'est possible, mais les distances sur
(genre d'(x,y) = |th(x) - th(y)|) ne sont pas des extensions de la distance usuelle sur
. Y a peut-être encore un moyen de s'en sortir et de passer de la continuité uniforme sur
à la continuité uniforme sur
, mais faudra le justifier et c'est pas la démarche attendue à mon avis.
Reste danset passe par les définitions epsilonesques. Si x et y sont suffisamment grands, tu peux utiliser la définition de la limite. Sinon, tu peux enfermer x et y dans un segment et utiliser l'uniforme continuité de f sur ce segment. Ça demande deux-trois manips mais ça doit marcher.
Ok, je me disais aussi que c'était un peu simple comme ça, merci de m'avoir accordé un peu de ton temps.
Tu peux aussi recopier la démonstration du théorème de Heine et changer ce qu'il faut pour que ça marche :
Tu prends > 0; tu recouvres
> 0; tu recouvres  par des intervalles I tels que f(I) est un intervalle ouvert de taille <
par des intervalles I tels que f(I) est un intervalle ouvert de taille <  /2, tu en extrais un recouvrement fini, et tu prends
/2, tu en extrais un recouvrement fini, et tu prends  = la moitié de la taille du plus petit intervalle que t'as pris, en considérant qu'un intervalle contenant l'infini est plus grand que tous les intervalles de R (de taille infinie)
= la moitié de la taille du plus petit intervalle que t'as pris, en considérant qu'un intervalle contenant l'infini est plus grand que tous les intervalles de R (de taille infinie)
Tu prends
Bonjour,
la démo peut se faire également à la main avec juste les définitions de sup.
Tu prends A>0 tel que-L| < \epsilon) .
.
Tu peux ensuite appliquer Heine sur le compact [0,A+1]. Ce qui permet de vérifier l'uniforme continuité (le "truc" est de prendre un module d'uniforme continuité )
)
Luc
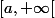 est un fermé de
est un fermé de 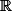 , non borné.
, non borné.
la démo peut se faire également à la main avec juste les définitions de sup.
Tu prends A>0 tel que
Tu peux ensuite appliquer Heine sur le compact [0,A+1]. Ce qui permet de vérifier l'uniforme continuité (le "truc" est de prendre un module d'uniforme continuité
Luc
Hazar a écrit:Bonjour,
Bonus : Pouvez vous me citer un fermé non borné "usuel" , je ne vois pas trop.
Hazar a écrit:Bon déja "R barre + est un compact", je n'en suis pas sûr, on nous a juste dit
que R barre en est un (je suis en MP), je suppose donc que "R barre +"
en est un aussi, mais, d'une façon générale je ne saisis pas trop en quoi R barre
est un fermé borné.
Il est pas fermé borné, il est compact. En règle générale dans les espaces topologiques les compacts ne sont pas les fermés bornés, c'est vrai pour les EVN de dimension finie mais on ne peut rien dire dans le cas général.
Pour voir qu'il est compact par exemple si tu le munis de la distance d(x,y)=|arctan(x)-arctan(y)| il est assez trivialement homéomorphe à [-Pi/2;Pi/2] qui est compact.
Sinon tu peux vérifier qu'une suite dans R barre a toujours une valeur d'adhérence en traitant les 2 cas possibles, suite bornée ou suite non bornée.
Bonus : Pouvez vous me citer un fermé non borné "usuel" , je ne vois pas trop.
Merci de m'éclairer !
Bah R est un fermé non borné par exemple.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
