Bon, toi et moi, on va redéfinir la notion de puissance, tu vas voir où ça coince.
Au début, on va travailler avec des exposants entiers.
Pour commencer, la toute première chose de base chez les puissance, c'est qu'on prend comme définition pour x réel et n entier
positif,
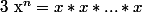
n fois.
Première
remarque, cette définition n'a pas de sens pour n=0.
Maintenant, les premières propriétés :
1) x^(n+k)=x^n*x^k pour n et k entiers positifs
démo : x^(n+k)=x*x*...*x n+k fois et par associativité x^(n+k)=(x*...*x)*(x*...*x) n et k fois, on a ce qu'on veut.
remarque : Cette démonstration, donc la propriété, n'a de sens que pour n et k non nuls
On pourrait de la même manière montrer que x^(n-k)=x^n/x^k lorsque n > k, la démonstration n'ayant toujours pas de sens pour n=k.
Ensuite, on veut étendre aux entiers négatifs. La définition x^n=x*...*x n fois n'aurait aucun sens. Comment définir x^n pour n négatif ? réponse : De façon à ce que les propriétés trouvées pour des entiers positifs marchent encore pour des entiers négatifs. Alors, pour que ça marche, on défini x^(-n) comme 1/x^n.
A ce stade, on sait toujours pas ce que vaut x^0.
On veut maintenant vérifier qu'avec cette définition, on peut bien étendre toutes les propriétés aux entiers négatifs et au mix des deux.
Si n-k > 0 : x^(n-k)=x*...*x n-k fois= (x*...*x n fois)/(x*...*x k fois) . Pas de sens pour n=k
Si n-k < 0 : x^(n-k)=1/(x*...x k-n fois)=(x*...*x n fois)/(x*...*x k fois). Toujours pas de sens pour n=k.
Bon, j'arrête, parce que je pense que tu as compris la chanson : La définition toute première des puissances exclue immédiatement la puissance nulle. Toutes les propriétés qui suivent ont un sens sauf pour ce cas.
Par contre, on remarque que si l'on avait posé dès le départ x^0=1, toutes les propriétés seraient vraies sans restriction, c'est bien pour cela qu'on pose x^0=1.
? Cette démonstration a-t-elle un sens lorsque n=k ?