Un probleme

[wserdx]

Bonjour
Je vous propose le résultat suivant:

[chan79]

Bonjour
Je vous propose le résultat suivant:

Joli calcul ! Bravo!

[kamel at]

cela dépasse le niveau lycée, mais résoudre le système du texte revient à chercher les points d'intersection de deux cubiques.
Il y a exactement 3 solutions: (-1,2) ,
et
Dans chaque cas, a²+b²=5

comment vous trouvez (-1:2)?

[kamel at]

Bonjour
Je vous propose le résultat suivant:

Merci beaucoup...

[chan79]

[quote="Iroh"]


QUOTE]
Une autre approche:
Si on considère que les égalités sont les équations de deux courbes, comme on cherche a²+b², on peut avoir l'idée de passer en coordonnées polaires
on pose x =
et y=
La première équation devient

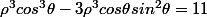
soit
On fait de même avec l'autre égalité et on obtient le système



Pour éliminer , on élève les deux égalités au carré et on additionne
on obtient après un peu de calcul (remplacer par )

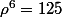
donc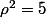
Comme TEX]\rho^2=a^2+b^2[/TEX] il est bien nécessaire que a²+b²=5
Pour déterminer les valeurs de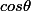 , on remplace dans la première égalité.
On doit alors utiliser la fastidieuse méthode de Cardan.
L'une des 3 solutions est
ce qui donne a= =-1
puis b=4

[chan79]

Merci beaucoup...

Ce qui suit est de niveau post-bac
Une autre approche:
Si on considère que les égalités sont les équations de deux courbes, comme on cherche a²+b², on peut avoir l'idée de passer en coordonnées polaires
on pose x =
et y=
La première équation devient

soit
On fait de même avec l'autre égalité et on obtient le système



Pour éliminer , on élève les deux égalités au carré et on additionne
on obtient après un peu de calcul (remplacer par )

donc
Comme il est bien nécessaire que a²+b²=5
Pour déterminer les valeurs de , on remplace dans la première égalité. On utilise la fastidieuse méthode de Cardan et on aboutit pour l’une des valeurs à
on arrive à (a,b)=(-1,2) les deux autres solutions se déduisent pas des rotations de 2pi/3

[Ericovitchi]

Sur le forum Ilesmaths, il y en a un qui a trouvé une solution simple :

ça donne le module de puis celui de a+ib : et on en déduit que a²+b²=5