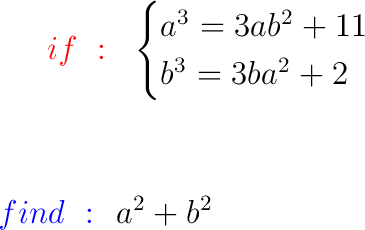Un probleme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kamel at
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Fév 2012, 21:17
-
 par kamel at » 02 Juin 2012, 13:55
par kamel at » 02 Juin 2012, 13:55
Bonjour
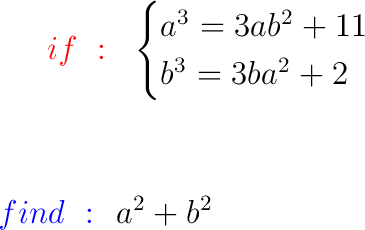
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 02 Juin 2012, 13:59
par Iroh » 02 Juin 2012, 13:59
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 13:59
par globule rouge » 02 Juin 2012, 13:59
Bonjour


Julie
-
kamel at
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Fév 2012, 21:17
-
 par kamel at » 02 Juin 2012, 14:01
par kamel at » 02 Juin 2012, 14:01
globule rouge a écrit:Bonjour

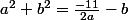
Julie
Moi j'ai trouvé que a²+b²=31b²
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 14:03
par globule rouge » 02 Juin 2012, 14:03
kamel at a écrit:Moi j'ai trouvé que a²+b²=31b²
Comment tu as fait ?

-
kamel at
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Fév 2012, 21:17
-
 par kamel at » 02 Juin 2012, 14:08
par kamel at » 02 Juin 2012, 14:08
globule rouge a écrit:Comment tu as fait ?

non, je fais une faute.
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 02 Juin 2012, 14:12
par Iroh » 02 Juin 2012, 14:12

et

différents de 0 sinon impossible.
On divise la première par

et la deuxième par

, on a:

On somme les deux:
 + 13)
On pose
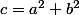
, on a:

D'où
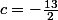
Sauf erreur.
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 14:14
par globule rouge » 02 Juin 2012, 14:14
Iroh a écrit:
et

différents de 0 sinon impossible.
On divise la première par

et la deuxième par

, on a:

On somme les deux:
 + 13)
On pose
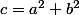
, on a:

D'où
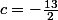
Sauf erreur.
Iroh, tu as oublié de diviser 11 et 2 par a et b dans la première ligne

-
kamel at
- Membre Naturel
- Messages: 26
- Enregistré le: 07 Fév 2012, 21:17
-
 par kamel at » 02 Juin 2012, 14:15
par kamel at » 02 Juin 2012, 14:15
Iroh a écrit:
et

différents de 0 sinon impossible.
On divise la première par

et la deuxième par

, on a:

On somme les deux:
 + 13)
On pose
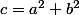
, on a:

D'où
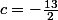
Sauf erreur.
vous oubliez de deviser 11 et 2 par a et b...
-
Iroh
- Membre Relatif
- Messages: 374
- Enregistré le: 14 Oct 2008, 19:24
-
 par Iroh » 02 Juin 2012, 14:17
par Iroh » 02 Juin 2012, 14:17
globule rouge a écrit:Iroh, tu as oublié de diviser 11 et 2 par a et b dans la première ligne

Ah oui, merci.
Du coup on arrive à
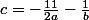
alors ?
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 14:19
par globule rouge » 02 Juin 2012, 14:19
Iroh a écrit:Ah oui, merci.
Du coup on arrive à
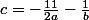
alors ?
Effectivement, et cela fait que j'avais inversé le

par inadvertance !
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 02 Juin 2012, 14:24
par sad13 » 02 Juin 2012, 14:24
Merci à tous, bel exo malgré qu'il paraît simple à la première vue.
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 02 Juin 2012, 14:30
par wserdx » 02 Juin 2012, 14:30
Avez-vous penser à utiliser
^3 = a^3-3a^2b+3ab^3-b^3$)
Cela permet de trouver

. Après je n'ai pas poussé d'autres calculs...
-
M@thIsTheBest
- Membre Relatif
- Messages: 318
- Enregistré le: 27 Déc 2011, 13:03
-
 par M@thIsTheBest » 02 Juin 2012, 14:39
par M@thIsTheBest » 02 Juin 2012, 14:39
kamel at a écrit:Bonjour
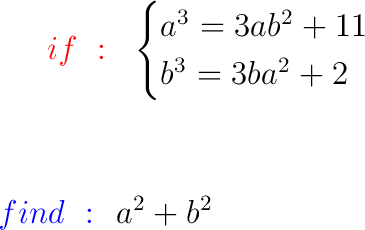
a et b sont des réelles ou des entiers ?
Sinon, on peut dire que
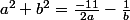
.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Juin 2012, 15:35
par chan79 » 02 Juin 2012, 15:35
kamel at a écrit:Bonjour
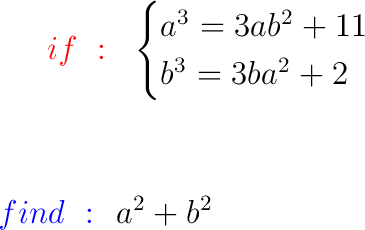
si (a,b)=(-1,2) ça marche et a²+b²=5
c'est pas grand'chose, mais c'est mieux que rien

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Juin 2012, 19:12
par chan79 » 02 Juin 2012, 19:12
chan79 a écrit:si (a,b)=(-1,2) ça marche et a²+b²=5
c'est pas grand'chose, mais c'est mieux que rien
cela dépasse le niveau lycée, mais résoudre le système du texte revient à chercher les points d'intersection de deux cubiques.
Il y a exactement 3 solutions: (-1,2) ,
)
et
)
Dans chaque cas, a²+b²=5
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 02 Juin 2012, 21:39
par manoa » 02 Juin 2012, 21:39
tient ça ma donné l'idée d'un système intéressant :
Résoudre dan R² le système :
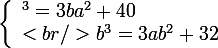
(copyright manoa :lol5: )

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 02 Juin 2012, 22:18
par chan79 » 02 Juin 2012, 22:18
manoa a écrit:tient ça ma donné l'idée d'un système intéressant :
Résoudre dan R² le système :
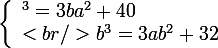
(copyright manoa :lol5: )
Par soustraction membre à membre
a³-b³=3ab(a-b)+8
(a-b)(a²+b²+ab-3ab)=8
(a-b)³=8
a-b=2
b=a-2
on remplace b dans la première égalité
avec un peu de patience (a,b)=(-2;-4)
sauf erreur de calcul, pas d'autre solution
-
manoa
- Membre Relatif
- Messages: 343
- Enregistré le: 12 Oct 2011, 00:02
-
 par manoa » 02 Juin 2012, 22:34
par manoa » 02 Juin 2012, 22:34
chan79 a écrit:Par soustraction membre à membre
a³-b³=3ab(a-b)+8
(a-b)(a²+b²+ab-3ab)=8
(a-b)³=8
a-b=2
b=a-2
on remplace b dans la première égalité
avec un peu de patience (a,b)=(-2;-4)
sauf erreur de calcul, pas d'autre solution
c'est bien ça

*l'idée était de remarquer les termes de l'identité remarquable (a-b)^3= a^3-3ba²+3b²a-b^3 .
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 02 Juin 2012, 22:34
par globule rouge » 02 Juin 2012, 22:34
Je trouve pareil !! :) Avec un peu (beaucoup) de retard ^^'
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités