Calcul de la somme des (-1)^n/(4n+1)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Stringer
- Membre Naturel
- Messages: 41
- Enregistré le: 26 Mai 2010, 16:52
-
 par Stringer » 31 Mai 2012, 17:18
par Stringer » 31 Mai 2012, 17:18
Bonjour, je suis face à un exercice ou il s'agit de calculer :

Pour l'instant j'ai écrit:

Mon soucis est que je n'arrive pas à justifier l'échange du signe somme et du signe intégral .
Je crois que le théorème d'interversion série intégrale sur un intervalle quelconque (on travail ici sur [0,1[ ne s'applique pas).
Quant au théorème de convergence dominée, je ne parviens pas à montrer l'hypothèse de domination. :marteau:
Un peu d'aide serait bienvenue :we:
Merci^^
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 31 Mai 2012, 18:06
par Skullkid » 31 Mai 2012, 18:06
Bonjour, le théorème d'interversion série-intégrale ne fonctionne en effet pas, parce que

diverge. Dans ton intégrale, le fait de travailler sur [0,1] ou [0,1[ ne change rien puisque l'intégrande est définie sur [0,1].
Il te reste la convergence dominée. Tu dois donc majorer
^k \right|)
par une quantité indépendante de n et intégrable vis-à-vis de t sur [0,1]. Utilise la formule donnant la somme des termes d'une suite géométrique.
-
lirabo
- Membre Naturel
- Messages: 39
- Enregistré le: 04 Jan 2010, 16:57
-
 par lirabo » 31 Mai 2012, 18:08
par lirabo » 31 Mai 2012, 18:08
Stringer a écrit:Bonjour, je suis face à un exercice ou il s'agit de calculer :

Pour l'instant j'ai écrit:

Mon soucis est que je n'arrive pas à justifier l'échange du signe somme et du signe intégral .
Je crois que le théorème d'interversion série intégrale sur un intervalle quelconque (on travail ici sur [0,1[ ne s'applique pas).
Quant au théorème de convergence dominée, je ne parviens pas à montrer l'hypothèse de domination. :marteau:
Un peu d'aide serait bienvenue :we:
Merci^^
Tu penses savoir integrer
)
entre 0 et 1 ?
Si oui, tu peux peut-être ne pas sommer jusqu'à l'infini mais N, inverser somme et intégrale.
et faire tendre N vers l'infini.
Sans garantie...
-
Stringer
- Membre Naturel
- Messages: 41
- Enregistré le: 26 Mai 2010, 16:52
-
 par Stringer » 31 Mai 2012, 19:27
par Stringer » 31 Mai 2012, 19:27
Rebonsoir, voici une majoration
.gif)
or 2/(1+t^4) est intégrable sur [0,1], donc on peut appliquer la convergence dominée et :
.gif)
d'ou :
.gif)
c'est ça ?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 31 Mai 2012, 19:33
par Skullkid » 31 Mai 2012, 19:33
C'est ça pour la majoration (y a ptet un problème dans tes majorations intermédiaires mais le majorant final est correct), le seul autre point à préciser pour satisfaire les hypothèses du théorème (et c'est juste là qu'il faut faire la distinction entre [0,1[ et [0,1] si on veut être parfaitement rigoureux) c'est que
^k)
converge bien simplement, sur [0,1[, vers

. Donc, tu trouves que
^n}{4n+1})
vaut l'intégrale de 1/(1+t^4) sur [0,1[, qui est évidemment égale à l'intégrale sur [0,1].
Après t'as plus qu'à t'amuser à calculer l'intégrale.
-
Stringer
- Membre Naturel
- Messages: 41
- Enregistré le: 26 Mai 2010, 16:52
-
 par Stringer » 31 Mai 2012, 19:39
par Stringer » 31 Mai 2012, 19:39
ah voila, c'est pour ça que je parlais de travailler sur [0,1[ plus tôt :we:
Sinon où vois tu un problème dans la majoration ?
Quant au calcul de l'intégrale, ça c'est un autre problème :mur:
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 31 Mai 2012, 19:44
par Skullkid » 31 Mai 2012, 19:44
Stringer a écrit:Sinon où vois tu un problème dans la majoration ?
Dans le calcul de la somme géométrique, au numérateur ce n'est pas t^(4n+1) mais t^(4n+4). Mais bon de toute façon le t disparaît après donc c'est pas bien grave.
-
Stringer
- Membre Naturel
- Messages: 41
- Enregistré le: 26 Mai 2010, 16:52
-
 par Stringer » 31 Mai 2012, 19:45
par Stringer » 31 Mai 2012, 19:45
Ah en effet, merci beaucoup :lol3:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 31 Mai 2012, 20:53
par chan79 » 31 Mai 2012, 20:53
Stringer a écrit:Ah en effet, merci beaucoup :lol3:
C'est peut-être un peu la même chose mais tant pis ...
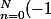^{n}}{4n+1})
=
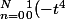^n)
dt=
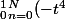^n)
dt=
^{N+1}}{1+t^4}dt)
=

-
^{N+1}}{1+t^4}dt)
La valeur absolue de la seconde intégrale se majore par

qui tend vers 0.
La limite cherchée est

Ensuite
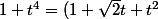(1-\sqr{2}t+t^2))
ce qui permet de transformer

en somme
-
lirabo
- Membre Naturel
- Messages: 39
- Enregistré le: 04 Jan 2010, 16:57
-
 par lirabo » 31 Mai 2012, 21:59
par lirabo » 31 Mai 2012, 21:59
chan79 a écrit:C'est peut-être un peu la même chose mais tant pis ...
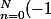^{n}}{4n+1})
=
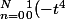^n)
dt=
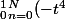^n)
dt=
^{N+1}}{1+t^4}dt)
=

-
^{N+1}}{1+t^4}dt)
La valeur absolue de la seconde intégrale se majore par

qui tend vers 0.
La limite cherchée est

Ensuite
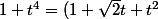(1-\sqr{2}t+t^2))
ce qui permet de transformer

en somme
Si j'en crois Wolfram Alpha, ça donnerait
-log(2-\sqrt2)+2.arctan(1+\sqrt2)-2.arctan(1-\sqrt2)))

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 01 Juin 2012, 06:31
par chan79 » 01 Juin 2012, 06:31
lirabo a écrit:Si j'en crois Wolfram Alpha, ça donnerait
2.arctan(1+\sqrt2)-2.arctan(1-\sqrt2))[/TEX]
oui, à partir de
=\sqr{2}-1)
et
=\sqr{2}+1)
, on peut montrer que
-2.arctan(1-\sqrt2))=\pi)
ce qui permet de présenter le résultat sous la forme :
)
=
+\pi))
-
Stringer
- Membre Naturel
- Messages: 41
- Enregistré le: 26 Mai 2010, 16:52
-
 par Stringer » 01 Juin 2012, 12:44
par Stringer » 01 Juin 2012, 12:44
chan79 a écrit:C'est peut-être un peu la même chose mais tant pis ...
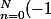^{n}}{4n+1})
=
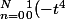^n)
dt=
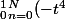^n)
dt=
^{N+1}}{1+t^4}dt)
=

-
^{N+1}}{1+t^4}dt)
La valeur absolue de la seconde intégrale se majore par

qui tend vers 0.
La limite cherchée est

Ensuite
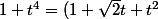(1-\sqr{2}t+t^2))
ce qui permet de transformer

en somme
Ah très bien, en fait j'essayais tellement d'appliquer un des gros théorèmes de spé que je pensais pas à ce genre de majoration simple. Merci beaucoup ! :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités



.gif)
.gif)
.gif)