DM: Suite géométrique (1°S)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kraki31
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Avr 2012, 16:27
-
 par kraki31 » 28 Mai 2012, 09:56
par kraki31 » 28 Mai 2012, 09:56
Bonjours à tous,
notre prof de maths à voulu nous donner un DM plutôt dur a faire car nous n'avons pas encore fini la leçon afin que nous nous préparions au futur contrôle. J'ai vraiment du mal un des exercices... Pourriez vous m'aidez à comprendre?
Voici l'énonce:
Un capital Co = 10 000 est placé sur un compte rapportant un intérêt de 4% par an.
À la fin de chaque année un montant de 20 est prélevé par la banque pour frais de gestion. On nomme Cn le montant disponible sur le compte à la fin de la n-ième année AVANT le prélèvement.
1)a) Calculer C1 puis C2: Sans trop de problème je trouve C1= 10 000x 4% + 10 000= 10 400
Puis C2=(C1-20)x4%+(C1-20)= 10 795,2
b) Justifier que Cn+1(n+1 en indice)= 1,04xCn-20,8: Cn+1=(1+4/100)x(Cn-20)=1,04Cn-20,8
Pouvez me confirmer cela et m'aider a ocmprendre la suite?
2) a) Posons Un=Cn-520 pour tout n>ou= à 0
b) Montrer que la suite (Un) est géométrique
c) Exprimer Un puis Cn en fonction de n. Puis déterminer avec la calculatrice au bout de combien d'année le capital initial aura t'il au moins doublé.
Merci de votre aide ! :we:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 10:52
par Dinozzo13 » 28 Mai 2012, 10:52
Salut !
Ca m'a l'air bon, toutefois, tu n'as pas besoin d'avoir répondu aux questions 1°)a) et 1°)b) pour répondre à la 2°)a) :++:
Utilise la définition d'une suite géométrique.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 28 Mai 2012, 10:53
par Joker62 » 28 Mai 2012, 10:53
Hello !
Le début est très bien.
Pour l'autre partie :
Pour montrer qu'une suite u_n est géométrique, il faut montrer qu'il existe q tel que u_(n+1) = q*u_n
Ici tu peux calculer u_(n+1) et essayer de l'exprimer en fonction de u_n
-
kraki31
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Avr 2012, 16:27
-
 par kraki31 » 28 Mai 2012, 11:28
par kraki31 » 28 Mai 2012, 11:28
J'ai fais essayer de cette façon mais je n'arrive pas à montrer que Un=qxUn :
Un=Cn-520
U_(n+1)= C_(n+1)-520
= 1,04Cn-20,8-520
= 1,04Cn-540,8
Je ne vois que cette façon vu qu'on nous demande d'exprimer Cn en fonction de n que dans les questions suivantes :/
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 12:21
par Dinozzo13 » 28 Mai 2012, 12:21
kraki31 a écrit:J'ai fais essayer de cette façon mais je n'arrive pas à montrer que Un=qxUn :
C'est
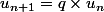
qu'il faut montrer, où q est une constante à déterminer.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 12:23
par Dinozzo13 » 28 Mai 2012, 12:23
kraki31 a écrit:U_(n+1)= C_(n+1)-520
= 1,04Cn-20,8-520
= 1,04Cn-540,8
Factorise par le coefficient devant Cn : 1,04 :++:
-
kraki31
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Avr 2012, 16:27
-
 par kraki31 » 28 Mai 2012, 12:26
par kraki31 » 28 Mai 2012, 12:26
D'accord merci je vais essayer ! Et donc pas besoin de se servir des réponses du 1) ?
Edit: je n'avais pas vu votre second post merci je vais faire ça !
-
kraki31
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Avr 2012, 16:27
-
 par kraki31 » 28 Mai 2012, 12:29
par kraki31 » 28 Mai 2012, 12:29
Du coup je trouve:
1,04(Cn-540,8/1,04)=1,04xUn
Correct? :)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 12:33
par Dinozzo13 » 28 Mai 2012, 12:33
voilà :k2k:
-
kraki31
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Avr 2012, 16:27
-
 par kraki31 » 28 Mai 2012, 12:45
par kraki31 » 28 Mai 2012, 12:45
Je trouve pour la question d'apres Un=9480x(1,04)^n
et Cn=9880x(1,04)^n + 520 il ne me reste plus qu'a rentrer Cn dans la calculette et relever pour quel n on obtient 20 000 ou plus ! :)
Est ce bien la marche à suivre?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 28 Mai 2012, 12:49
par Dinozzo13 » 28 Mai 2012, 12:49
kraki31 a écrit:(...) Cn=9880x(1,04)^n + 520 (...) Est ce bien la marche à suivre?
Tu veux dire
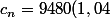^n+520)
!
Oui, c'est bon :+++:
-
kraki31
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Avr 2012, 16:27
-
 par kraki31 » 28 Mai 2012, 12:53
par kraki31 » 28 Mai 2012, 12:53
Oui faute de frappe ! ^^
-
kraki31
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Avr 2012, 16:27
-
 par kraki31 » 28 Mai 2012, 12:59
par kraki31 » 28 Mai 2012, 12:59
Je trouve C19= 20 493 et C18<20 000 donc le capital double au bout de 19ans ! :)
Merci à toi !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
