Equadiff - transformation en polaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 26 Mai 2012, 10:58
par acoustica » 26 Mai 2012, 10:58
Yop yop ! :zen:
J'ai fais un pitite équation différentielle, je bloque. Toute aide est la plus que bienvenue ! (et d'ailleurs si quelqu'un a une référence particulièrement claire et pédagogique que le calcul différentiel, je suis preneur !)
On a donc cette équadiff :
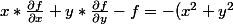)
Donc évidemment, transformée en polaires :
=f(r*cos{\theta),r*sin{\theta})=F(r,\theta))
On a :
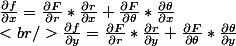
avec :
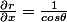
Soit :
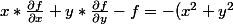\\<br /> r*cos \theta [\frac{\partial F}{\partial r}*\frac{1}{cos \theta} + \frac{\partial F}{\partial \theta}*\frac{\partial \theta}{\partial x}]+r*sin \theta [\frac{\partial F}{\partial r}*\frac{1}{sin \theta} + \frac{\partial F}{\partial \theta}*\frac{\partial \theta}{\partial y}] <br />-F= -r^2)
d'où :
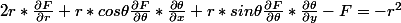
Et là ben... je sais pas.
-
JeanJ
- Membre Relatif
- Messages: 264
- Enregistré le: 09 Jan 2010, 09:04
-
 par JeanJ » 26 Mai 2012, 11:44
par JeanJ » 26 Mai 2012, 11:44
acoustica a écrit:Yop yop ! :zen:
J'ai fais un pitite équation différentielle, je bloque. Toute aide est la plus que bienvenue ! (et d'ailleurs si quelqu'un a une référence particulièrement claire et pédagogique que le calcul différentiel, je suis preneur !)
On a donc cette équadiff :
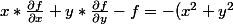)
Donc évidemment, transformée en polaires :
=f(r*cos{\theta),r*sin{\theta})=F(r,\theta))
On a :
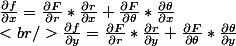
avec :
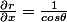
Soit :
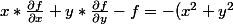\\<br /> r*cos \theta [\frac{\partial F}{\partial r}*\frac{1}{cos \theta} + \frac{\partial F}{\partial \theta}*\frac{\partial \theta}{\partial x}]+r*sin \theta [\frac{\partial F}{\partial r}*\frac{1}{sin \theta} + \frac{\partial F}{\partial \theta}*\frac{\partial \theta}{\partial y}] <br />-F= -r^2)
d'où :
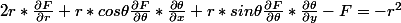
Et là ben... je sais pas.
Vous n'y arriverez pas de cette façon si vous n'avez pas calculé préalablement
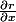
,
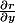
,
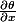
et
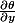
en fonction de r et de

(votre
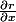
est faux)
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 26 Mai 2012, 12:18
par acoustica » 26 Mai 2012, 12:18
JeanJ a écrit:Vous n'y arriverez pas de cette façon si vous n'avez pas calculé préalablement
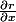
,
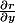
,
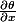
et
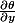
en fonction de r et de

(votre
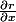
est faux)
Bonjour,
Merci pour votre réponse. Je viens de comprendre pourquoi mon dr/dx est faux. J'avais multiplié en haut et en bas par
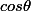
, mais je ne peux bien sur pas faire rentrer le
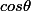
aux côtés du r. Partant de là je m'escrimais à essayer de montrer que le résidu était nul, ce qu'il n'a aucune raison d'être. Merci à vous, je vais me replonger dans tout ça.
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 28 Mai 2012, 11:47
par egan » 28 Mai 2012, 11:47
Personnellement, je ne suis pas le plus grand fan du passage en polaires. D'ailleurs, si le second membre ne ressemblait pas à r^2, tu n'aurais pas eu, je pense l'idée de passer en polaires. Une méthode plus générale consiste à chercher une fonction g de R^2 dans R^2 telle que la dérivée par rapport à x de fog ressemble à s'y méprendre à x.df/dx+y.df/dy. Je te laisse y réfléchir. Demande moi si tu bloqués pour trouver g.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
