Bonjour à tous,
Je me permet de vous soumettre un petit problème de 2 équations à 2 inconnues.
Un élève me l'a soumis (oui, je suis prof !) mais je pense qu'il manque peut-être une donnée... ou alors, le soleil m'a-t-il trop tapé sur la tête de sorte que je ne sache plus réfléchir? Hum...
Voici:
Pierre n'habite pas très loin de chez son grand-père. Hier, il lui a téléphoné pour lui dire qu'il lui rendrait une visite. "Je viendrai à ta rencontre; et ensemble, nous retournerons chez moi. Je partirai à 4h15" lui dit pépé. Pierre lui a répondu: "Moi, je partirai à quatre heures".
A quelle distance Pierre habite-t-il de chez son grand-père si tu sais que Pierre se déplace à 4km/h, que son grand-père se déplace à 3km/h et que, une fois rentré chez lui, Pierre a parcouru une distance 4 fois plus grande que son grand-père?
D'avance merci pour vos réponses !
Problème 2éq à 2 inconnues "impossible"? à résoudre
7 messages
- Page 1 sur 1
Hello,
Et bien X la distance de chez Pierre à son grand-père.... et Y la distance parcourue par le grand-père peut-être?
Sérieux je patauge, quelle honte !
Je vois pas ce que la vitesse vient faire là)dedans si on ne nous dit pas une heure de rencontre...
Et bien X la distance de chez Pierre à son grand-père.... et Y la distance parcourue par le grand-père peut-être?
Sérieux je patauge, quelle honte !
Je vois pas ce que la vitesse vient faire là)dedans si on ne nous dit pas une heure de rencontre...
jamys123 a écrit:Yop,
T'as posé quels inconnues, quels équations...
Personnellement, je pose le problème comme suit :
Soit la distance séparant la maison de Pierre du point de rencontre avec son grand-père et
la distance séparant la maison de Pierre du point de rencontre avec son grand-père et 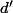 celle séparant la maison du grand-père de ce même point.
celle séparant la maison du grand-père de ce même point.
Pierre va faire dans la journée un trajet égal à) qui correspond à un aller-retour entre chez lui et chez son grand père.
qui correspond à un aller-retour entre chez lui et chez son grand père.
Le grand père fait dans la journée un trajet égal à qui correspond à un aller-retour entre chez lui et le point où il rencontre son petit-fils.
qui correspond à un aller-retour entre chez lui et le point où il rencontre son petit-fils.
On a donc :=4\times \cancel 2 d'\;\Rightarrow\; d'=\dfrac{d}{3} \qquad (1))
On nous dit ensuite que :
Cela signifie que, pour se retrouver au même moment au point de rencontre (c'est le principe d'une rencontre; si on n'est pas au même moment au même endroit, ça pose problème pour se voir), il faut que Pierre parte un quart d'heure plus tôt que son papi, durant lequel il parcourt . En se basant sur le moment où le grand-père part de chez lui, on a donc :
. En se basant sur le moment où le grand-père part de chez lui, on a donc :

En utilisant) on peut alors remplacer
on peut alors remplacer 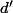 dans cette expression qui nous donne :
dans cette expression qui nous donne :

En utilisant à nouveau) , on trouve ensuite
, on trouve ensuite 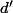 :
:  .
.
Enfin, le distance séparant la maison de Pierre de celle de son papi est donc égale à .
.
Pas besoin de donnée supplémentaire :lol3:
Soit
Pierre va faire dans la journée un trajet égal à
Le grand père fait dans la journée un trajet égal à
[...]une fois rentré chez lui, Pierre a parcouru une distance 4 fois plus grande que son grand-père
On a donc :
On nous dit ensuite que :
"Je partirai à 4h15" lui dit pépé. Pierre lui a répondu: "Moi, je partirai à quatre heures"
Cela signifie que, pour se retrouver au même moment au point de rencontre (c'est le principe d'une rencontre; si on n'est pas au même moment au même endroit, ça pose problème pour se voir), il faut que Pierre parte un quart d'heure plus tôt que son papi, durant lequel il parcourt
En utilisant
En utilisant à nouveau
Enfin, le distance séparant la maison de Pierre de celle de son papi est donc égale à
Pas besoin de donnée supplémentaire :lol3:
calolda a écrit:Hello,
Et bien X la distance de chez Pierre à son grand-père.... et Y la distance parcourue par le grand-père peut-être?
Sérieux je patauge, quelle honte !
Je vois pas ce que la vitesse vient faire là)dedans si on ne nous dit pas une heure de rencontre...
Salut
x distance de la maison du grand-père au point de rencontre R
y distance de la maison de Pierre au point de rencontre R
si t est le temps mis par le grand père pour aller de sa maison au point R, Pierre met le temps t+1/4 pour aller de sa maison à R
il reste à poser trois équations et à résoudre
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 106 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
