Equation du type n^x
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
penofchaos
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2012, 16:26
-
 par penofchaos » 26 Mai 2012, 17:25
par penofchaos » 26 Mai 2012, 17:25
Bonjour,
Voilà j'ai un soucis avec un exercice je ne trouve pas la solution attendue

Voici l'équation sur ce lien:
http://dom-apps.unibocconi.it/BOC/1112/30063_s2.nsf/$KeyAttach/20120522-120148-9388/$FILE/homework6engsol.pdf?OpenElement C'est l'exercice 2, question b. Je comprends pas comment ils trouvent cette solution pour i
A étant une constante, je dois isoler i.
Je pensais à celà:
En divisant par C des deux cotés, pour plus de compréhension, je nommerai A le terme qui est à gauche de l'équation, divisé par A qui se trouvait à droit, ensuite:
e(2n*LN(1+i))=A
Ln( e(2n*LN(1+i)) ) = Ln(A)
2n*Ln(1+i)=Ln(A)
Ln(1+i)=Ln(A)/(2n)
1+i=e( Ln(A) / (2n))
et donc
i= e(Ln(A)/(2n))-1
Je ne comprends pas comment il faut faire :/
merci !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Mai 2012, 17:43
par Kikoo <3 Bieber » 26 Mai 2012, 17:43
Yo

Alors tu pars de la relation
^{2n}=C(1+i')^n(1+i'')^n)
On simplifie par C comme tu l'as fait !
On applique la racine 2-nième sur les deux membres (cela fait
^{2n}}=\sqrt[2n]{(1+i')^n(1+i'')^n})
)
Et les puissances n-ième s'annulent à droite. Il ne reste plus que la racine carrée !
D'où
(1+i'')})
...
Et on conclut
-
penofchaos
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2012, 16:26
-
 par penofchaos » 26 Mai 2012, 18:01
par penofchaos » 26 Mai 2012, 18:01
Kikoo <3 Bieber a écrit:Yo

Alors tu pars de la relation
^{2n}=C(1+i')^n(1+i'')^n)
On simplifie par C comme tu l'as fait !
On applique la racine 2-nième sur les deux membres (cela fait
^{2n}}=\sqrt[2n]{(1+i')^n(1+i'')^n})
)
Et les puissances n-ième s'annulent à droite. Il ne reste plus que la racine carrée !
D'où
(1+i'')})
...
Et on conclut
Merci pour ta réponse rapide !
Ok je ne connaissais pas ces racines 2-nième, apparemment en l'applicant sur le membre de gauche on passe de puissance n à racine carrée. Je vais chercher des infos sur cela car je connais pas.
Mais c'est curieux mon raisonnement est faux ? Pourtant il me semble bien que a^x=e(xlna).
Bon en tout cas merci pour la réponse je vais tenter de comprendre
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 26 Mai 2012, 18:14
par Kikoo <3 Bieber » 26 Mai 2012, 18:14
Ah, ok ^^ Si tu ne connais pas la fonction racine n-ième, dis-toi que c'est la fonction réciproque de la fonction puissance de n.
On arrive à ce résultat en passant par l'exponentielle, en effet, pour plus de rigueur :
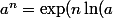))
On cherche la fonction F qui appliquée sur
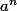
donnera a.
Cela équivaut à chercher F tel que
)]=a)
On se rend compte que
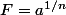
fonctionne car
)]^{1/n}=\exp\left(n\times \frac{1}{n}\ln(a)\right)=\exp(\ln(a))=a)
-
penofchaos
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2012, 16:26
-
 par penofchaos » 26 Mai 2012, 18:22
par penofchaos » 26 Mai 2012, 18:22
Kikoo <3 Bieber a écrit:Ah, ok ^^ Si tu ne connais pas la fonction racine n-ième, dis-toi que c'est la fonction réciproque de la fonction puissance de n.
On arrive à ce résultat en passant par l'exponentielle, en effet, pour plus de rigueur :
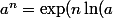))
On cherche la fonction F qui appliquée sur
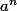
donnera a.
Cela équivaut à chercher F tel que
)]=a)
On se rend compte que
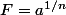
fonctionne car
)]^{1/n}=\exp\left(n\times \frac{1}{n}\ln(a)\right)=\exp(\ln(a))=a)
Aaaaaaaaaaaaaaaaah

Voilà quelques clarifications qui expliquent tout !!
Merci beaucoup j'ai compris mnt, un grand merci :p
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 26 Mai 2012, 18:33
par el niala » 26 Mai 2012, 18:33
penofchaos a écrit:Aaaaaaaaaaaaaaaaah

Voilà quelques clarifications qui expliquent tout !!
Merci beaucoup j'ai compris mnt, un grand merci :p
pour compléter la réponse de
Kikoo <3 Bieber si c'est la notion de "racine nième" qui te dérange, écris simplement avec la fonction puissance "rationnelle" puisqu'en finances tu sais que le radicande est positif
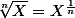
et là c'est immédiat
^{2n}\)^{\frac{1}{2n}} = \(\not{C} (1 + i^')^n (1 + i^{''})^n\)^{\frac{1}{2n}})
-
penofchaos
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Avr 2012, 16:26
-
 par penofchaos » 26 Mai 2012, 20:33
par penofchaos » 26 Mai 2012, 20:33
el niala a écrit:pour compléter la réponse de
Kikoo <3 Bieber si c'est la notion de "racine nième" qui te dérange, écris simplement avec la fonction puissance "rationnelle" puisqu'en finances tu sais que le radicande est positif
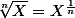
et là c'est immédiat
^{2n}\)^{\frac{1}{2n}} = \(\not{C} (1 + i^')^n (1 + i^{''})^n\)^{\frac{1}{2n}})
Merci x^1/n me parle beaucoup plus

Je comprends mieux mnt.
Mais dernière chose, pour celui ou celle qui a le courage par hasard de me dire qu'est ce qui est faux dans mon développement à moi ? J'ai forcémment du écrire des choses fausses :p
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
