Intégrale généralisée

[Mysterion]

Je me tire les cheveux depuis une heure à essayer de résoudre ce petit problème :



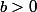
et . Déterminer l'ensemble des couples pour lesquels l'intégrale généralisée est convergentes.

Je l'ai majorer par , fait une IPP .

J'applique le critère de Riemann pour l'intégrale de droite en et ]0,1]. J'obtiens :

pour tout t compris entre 1 et -a+b > 0
pour tout t compris entre 0 et 1 -a+b 1.
En 0, la condition sur a et b est a > 1.

Bref, je suis complètement à coté de la plaque.

[gdlrdc]

1)Bon alors évacuons les problèmes en 0:
b est positif donc le dénominateur tend vers 1 en 0 donc pas de problème,
Au numérateur t^a l'emporte sur lnt, donc
1i)si a positif pas de problème ça tend vers 0 donc la fonction est intégrable en 0
1ii) si a est négatif ou nul, ça tend vers + l'infini donc pas intégrable en 0

2) le problème en + l'infini
la fonction est équivalente à t^(a-b)lnt , avec Riemann tu en déduis que l'intégrale converge en +infini pour a-b plus petit que -1.

3) conclusion 0 inférieur à a inférieur à b-1

A toi de rédiger proprement en langage mathématique.

[Mysterion]

Bonjour,

Merci pour ta réponse tout est claire à l’exception d'une chose. Selon le critère de Riemann pour t compris entre 0 et 1, l'intégrale de 1/t^(b-a) converge si b-a < 1. Ici on étudie la convergence de l'intégrale sur [0 l'infini]. Ne devrions nous pas séparer les intervalles ? Un truc m’échappe...