Esperance

par **snake974** » 23 Juin 2006, 18:24

Bonjour, je butte sur un exercice de probabilité dont voici l'enoncé:

On considere une suite infinie d'experiences de Bernoullo indépendantes et de même parametre p (0Soit X indice i la variable de Bernoulli definie par X indice i =1 ssi la ieme exp de Bernoulli est un succès.
S1 designe le rang du premier succés;
Donner la distribution de S1 et montrer que E(S1(S1-1))=(2*(1-p))/p^2.

J'ai trouvé pour la distribution de S1 q^(k-1)*p.

Merci d'avance

par **buzard** » 23 Juin 2006, 23:06

bonjour,

pour faire simple rapplel toi la serie géometrique, tu aboutiras vite au résultat. Sinon tu peut utiliser la sommation par partie d'abel, mais là c'est plus long les calculs ...

pour les incultes la série géometrique c'est :

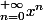
par **Daragon geoffrey** » 24 Juin 2006, 09:59

slt
tu peux aussi construire un arbre des probas, le nombre d'expèrience est infinie elles sont indépendantes 2 à 2 et avec seulement 2 issues possibles, succès ou éhec, de plus X(i=1) a pour proba : on note f : "succès à la ième itération", alors f(barre) : "échec sur les (i-1)ième première itération)", donc la proba demandée est p(Xi=1)=1-(1-p)^(i-1), à partir de là, tu calcules l'espérnce, la variance, ... la distribition et ainsi de suite ! @ +

par **snake974** » 25 Juin 2006, 07:23

Je suis désolé mais je n'y arrive pas :triste: .
Merci quand meme

par **buzard** » 25 Juin 2006, 10:54

Le but de cet exercice et de faire prendre conscience que l'esperance de la loi de bernouilli se calcul plus facilement si tu remarque qu'avec :

en dérivant tu obtient :

f'(x) te permet de calculer E[S1]
f"(x) de calculer E[S1(S1-1)]
et ainsi de suite

en poussant les calculs tu peut meme calculer E[S1!] mais ca demande un peut d'habilité et ca sert pas à grand chose.

par **snake974** » 25 Juin 2006, 12:29

Merci beaucoup je' n'avais pas pensé aux DSE

Esperance

Esperance

Qui est en ligne