Petite question autour de Z[i]

[waddle30]

salut tout le monde.
j'ai un petit problème concernant l'anneau Z[i]concrètement on doit montrer qu'il est principale,je comprend la méthode mais il y a un petit détail qui mérite d’être expliqué je pense.
donc on a Z[i]={a+ib/(a,b) dans Z²) et I idéal de Z[i], J={yz0/y dans Z[i]} et |z0|²=n
on définit T={|z|²/z dans I,z#0}
n=min T
pour tout x de I*
P={|x-t|/t dans J}
ñ=min P
comment montre t-on que ñ<(ou égal)n ?

notre prof à fait un schéma puis a dit "on voit clairement que ñ<(ou égal)n",je suis désolé mais un schéma n'est en aucun cas une démonstration :mur:
pouvez vous m'aidez s'il vous plait?
merci par avance :lol3:

[waddle30]

vérifie ()
est inclus dans
et idéal de , et
on définit

pour tout de

[alm]

Bonjour :

Une réponse à ta question est basée sur ce qui suit:

Si est un nombre complexe tel que et si on pose : 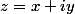réels et et repectivement les parties entières de et et si on considére les quatre éléments de


Essaye de tracer un schéma, tu verra que est un carré dont le domaine contient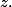

Votre professeur vous aurait expliqué que la distance de à l'une au moins des extrimités de ce carré à savoi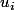r pour , cette distance est strictement plus petite que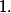

Puisque tu veux une démo précise tu as tout pour la faire , à savoir:

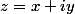et et ne sont pas simultanément entiers et :

et

si forcément tu calcule par exemple tu verra que c'est

Si même raisonnement tu as
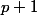Si ni ni n'est entier alors tu prends l'entier le plus proche à d'entre et et l'entier le plus proche à d'entre et 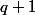tu prouves que réponds au problème



Ainsi on démontré :


Lemme :
Pour tout nombre complexe il existe au moins tel que .

Soit alors un idéal non nul de
Alors est une partie non vide de 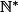, elle admet un plus petit élément, autrement il existe tel que :
.

On va montrer que .
Soit alors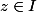
1es cas : si c'est terminé.
2e cas: sinon d'aprés le lemme il existe au moins tel que :
Poson :
Alors : si bien que (on attire l'attention ici que est un idéal de et comme et on a )
On a puique il est supposé que
Par définition de on a alors : donc , ce qui contredit .
Il en résulte que le 2eme cas ne peut avoir lieu et on a ce qu'on désire démontrer.