Bonne chance
Arithmétique - I
11 messages
- Page 1 sur 1
Arithmétique - I
Montrer que pour tout entier  (
(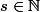 ), il existe un entier
), il existe un entier  divisible par
divisible par  et dont la somme des chiffres soit égale a
et dont la somme des chiffres soit égale a  (
( est écrit dans le système décimal).
est écrit dans le système décimal).
Bonne chance (exercice assez difficile)
(exercice assez difficile)
Bonne chance
Une réponse partielle :
Supposons p premier différent de 2 et 5. Je considère le nombre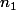 écrit avec
écrit avec  chiffres 1, et j'appelle r son reste modulo p (je le suppose non nul pour l'instant).
chiffres 1, et j'appelle r son reste modulo p (je le suppose non nul pour l'instant).
Je sais que est congru à 1 modulo p, et en supposant que 10 est un générateur du groupe multiplicatif de Z/pZ, une des puissances de 10 à partir de
est congru à 1 modulo p, et en supposant que 10 est un générateur du groupe multiplicatif de Z/pZ, une des puissances de 10 à partir de  sera congrue à -r modulo p. Finalement, en metant un 1 à cet endroit, puis des zéros et ma suite de
sera congrue à -r modulo p. Finalement, en metant un 1 à cet endroit, puis des zéros et ma suite de  chiffres 1, je forme bien un nombre dont la somme des chifres est p , et multiple de p
chiffres 1, je forme bien un nombre dont la somme des chifres est p , et multiple de p
Le problème, c'est que 10 n'est pas toujours générateur du groupe multiplicatif, par exemple pour p =13
J'en suis là pour l'instant
Je pense quand même qu'on doit pouvoir fabriquer ce nombre en utilisant seulement les chiffres 0 et 1, et étendre à n'importe quelle base de numération
Gqlt
Supposons p premier différent de 2 et 5. Je considère le nombre
Je sais que
Le problème, c'est que 10 n'est pas toujours générateur du groupe multiplicatif, par exemple pour p =13
J'en suis là pour l'instant
Je pense quand même qu'on doit pouvoir fabriquer ce nombre en utilisant seulement les chiffres 0 et 1, et étendre à n'importe quelle base de numération
Gqlt
Je ne pense pas que ça marchera juste pour les nombres composés de  et
et  , par example si on prend le nombre
, par example si on prend le nombre  , on a
, on a 
Mais la méthode que vous avez appliquée dépasse le niveau où on est, peut être on aura ça en terminale, cependant, je n'ai rien pigé de la démonstration.
Moi j'ai essayé avec des polynômes,


Donc



Par la division euclidienne, je dois trouver un polynôme dont les coefficient sont des entiers, et à la fin, on donne et d'ici, la troisème polynôme
et d'ici, la troisème polynôme  sera de
sera de  pour
pour  égale à un certain nombre (
égale à un certain nombre ( par example), mais jusqu'à mnt, la division me conduit vers des déductions lointaine. Peut être le chemin est long, mais donnez moi votre avis, merci en avance. Ah ! tjrs je cherche une autre méthode plus simple, peut être je garde les polynômes mais je simplifie la méthode (si le mot simplifier va dans cette place, lol)
par example), mais jusqu'à mnt, la division me conduit vers des déductions lointaine. Peut être le chemin est long, mais donnez moi votre avis, merci en avance. Ah ! tjrs je cherche une autre méthode plus simple, peut être je garde les polynômes mais je simplifie la méthode (si le mot simplifier va dans cette place, lol)
merci
 et
et  , par example si on prend le nombre
, par example si on prend le nombre  , on a
, on a 
Mais la méthode que vous avez appliquée dépasse le niveau où on est, peut être on aura ça en terminale, cependant, je n'ai rien pigé de la démonstration.
Moi j'ai essayé avec des polynômes,



Donc




Par la division euclidienne, je dois trouver un polynôme dont les coefficient sont des entiers, et à la fin, on donne
 et d'ici, la troisème polynôme
et d'ici, la troisème polynôme  sera de
sera de  pour
pour  égale à un certain nombre (
égale à un certain nombre ( par example), mais jusqu'à mnt, la division me conduit vers des déductions lointaine. Peut être le chemin est long, mais donnez moi votre avis, merci en avance. Ah ! tjrs je cherche une autre méthode plus simple, peut être je garde les polynômes mais je simplifie la méthode (si le mot simplifier va dans cette place, lol)
par example), mais jusqu'à mnt, la division me conduit vers des déductions lointaine. Peut être le chemin est long, mais donnez moi votre avis, merci en avance. Ah ! tjrs je cherche une autre méthode plus simple, peut être je garde les polynômes mais je simplifie la méthode (si le mot simplifier va dans cette place, lol)merci
Je n'écris que des conneries
Quand p est premier (diférent de 2, 3 ou 5), le nombre composé de chiffres 1 est toujours un multiple de p (puisqu'il vaut
chiffres 1 est toujours un multiple de p (puisqu'il vaut  ) et que justement, p étant premier,
) et que justement, p étant premier,  est congru à 1 modulo p, et donc mon reste est nul. Je ne peux donc pas ajouter de chiffre 1 à gauche si facilement. Je décale donc le dernier 1 vers la gauche. Pour l'instant, la somme des chiffres est
est congru à 1 modulo p, et donc mon reste est nul. Je ne peux donc pas ajouter de chiffre 1 à gauche si facilement. Je décale donc le dernier 1 vers la gauche. Pour l'instant, la somme des chiffres est  , et mon nombre(1011...1) s'écrit donc
, et mon nombre(1011...1) s'écrit donc  , il est donc congru à
, il est donc congru à  soit à 9 modulo p.
soit à 9 modulo p.
Si maintenant je peux trouver une puissance de 10 congrue à -9 modulo p je vais m'en sortir.
Quand p est premier (diférent de 2, 3 ou 5), le nombre composé de
Si maintenant je peux trouver une puissance de 10 congrue à -9 modulo p je vais m'en sortir.
Peut être j'ai une diée, est-ce qu'on peut démontrer par récurrence ? j'ai essayé par récurrence et peut être ça marche, bon je vais l'écrire.
Pour le nombre

 ,
,  (p)
(p)
[indent]Pour
[/indent] et
et 
 et par conséquent, le quotient donne
et par conséquent, le quotient donne  qui est un entier
qui est un entier
On suppose (p). Soit un entier.
un entier.

... à la fin on trouve que c'est vérfié pour ou
ou 
Mais bon, je ne suis pas sûr
Pour le nombre


 ,
,  (p)
(p)[indent]Pour

[/indent]
 et
et 
 et par conséquent, le quotient donne
et par conséquent, le quotient donne  qui est un entier
qui est un entierOn suppose (p). Soit
 un entier.
un entier.

... à la fin on trouve que c'est vérfié pour
 ou
ou 
Mais bon, je ne suis pas sûr
A mesure que je deviens vieux
Je m'en aperçois mieux
J'ai le cerveau qui flanche
Soyons sérieux disons le mot
C'est même plus un cerveau
C'est comme de la sauce blanche (Boris Vian)
Si p est premier (diférent de 2 ou 5), il existe une puissance de 10 congrue à 1 modulo p (au pire ). appelons la k . Il est évident que
). appelons la k . Il est évident que 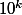 ,
, 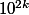 ...
... sont tous congrus à 1 modulo p, et leur somme
sont tous congrus à 1 modulo p, et leur somme  est donc congrue à p modulop , et a bien pour somme des chiffres p
est donc congrue à p modulop , et a bien pour somme des chiffres p
Pour un nombre non premier, je continue à chercher
Galt
Je m'en aperçois mieux
J'ai le cerveau qui flanche
Soyons sérieux disons le mot
C'est même plus un cerveau
C'est comme de la sauce blanche (Boris Vian)
Si p est premier (diférent de 2 ou 5), il existe une puissance de 10 congrue à 1 modulo p (au pire
Pour un nombre non premier, je continue à chercher
Galt
Je le tiens (mais qu'est ce que ça a été laborieux)
Si 10 est premier avec s , alors il existe une puissance de 10 (différente de 1) congrue à 1 modulo s . En effet, les s nombres ne peuvent pas avoir de reste nul dans la division par s , deux restes sont donc égaux. On a donc
ne peuvent pas avoir de reste nul dans la division par s , deux restes sont donc égaux. On a donc  modulo s , donc
modulo s , donc  modulo s . Appelons donc k cette puissance. Les s nombres 1,
modulo s . Appelons donc k cette puissance. Les s nombres 1, 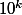 ,
, 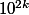 ...
...k}) sont tous congrus à 1 modulo s , leur somme est un multiple de s , et elle s'écrit avec s chifres 1 (et un paquet de chiffres 0).
sont tous congrus à 1 modulo s , leur somme est un multiple de s , et elle s'écrit avec s chifres 1 (et un paquet de chiffres 0).
Si maintenant 10 n'est pas premier avec s , on écrit avec q premier avec 10, on écrit le nombre multiple de q avec q chiffres 1, qu'on répète
avec q premier avec 10, on écrit le nombre multiple de q avec q chiffres 1, qu'on répète  fois pour que la somme des chiffres soit s . C'est encore un multiple de q . Pour en faire un multiple de s , on ajoute autant de zéros qu'il le faut à droite (sup (a ,b ).
fois pour que la somme des chiffres soit s . C'est encore un multiple de q . Pour en faire un multiple de s , on ajoute autant de zéros qu'il le faut à droite (sup (a ,b ).
Cette démonstration marche pour toutes les bases
Ouf
Si 10 est premier avec s , alors il existe une puissance de 10 (différente de 1) congrue à 1 modulo s . En effet, les s nombres
Si maintenant 10 n'est pas premier avec s , on écrit
Cette démonstration marche pour toutes les bases
Ouf
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
