DM Suites & Intégrales
14 messages
- Page 1 sur 1
DM Suites & Intégrales
Bonjour à tous,
J'ai un petit problème pour un DM qui est à faire pour demain, et je vous sollicite afin de m'éclairer sur le sujet. :langue:
On définit la suite u par u0 = intégrale de 0 à 1 de 1/(20-x) dx et, pour tout entier naturel non nul n, un = intégrale de 0 à 1 de x^n/(20-x) dx.
1-On a prouvé que u0 = ln(20/19)
2-En divisant x par -x + 20, calculer u1
En divisant x² par -x + 20, calculer u2
3- On généralise la méthode initiée à la question 2 ; prouver que pour n >= à 0 on a :
x^(n+1) = (x^n)(x-20) + 20x^n .
En déduire que pour n>= 0 on a : un+1 = 20un - 1/(n+1)
Voilà , je suis bloqué pour cette partie, merci d'avance pour votre aide :we:
J'ai un petit problème pour un DM qui est à faire pour demain, et je vous sollicite afin de m'éclairer sur le sujet. :langue:
On définit la suite u par u0 = intégrale de 0 à 1 de 1/(20-x) dx et, pour tout entier naturel non nul n, un = intégrale de 0 à 1 de x^n/(20-x) dx.
1-On a prouvé que u0 = ln(20/19)
2-En divisant x par -x + 20, calculer u1
En divisant x² par -x + 20, calculer u2
3- On généralise la méthode initiée à la question 2 ; prouver que pour n >= à 0 on a :
x^(n+1) = (x^n)(x-20) + 20x^n .
En déduire que pour n>= 0 on a : un+1 = 20un - 1/(n+1)
Voilà , je suis bloqué pour cette partie, merci d'avance pour votre aide :we:
turt a écrit:Bonjour à tous,
J'ai un petit problème pour un DM qui est à faire pour demain, et je vous sollicite afin de m'éclairer sur le sujet. :langue:
On définit la suite u par u0 = intégrale de 0 à 1 de 1/(20-x) dx et, pour tout entier naturel non nul n, un = intégrale de 0 à 1 de x^n/(20-x) dx.
1-On a prouvé que u0 = ln(20/19)
2-En divisant x par -x + 20, calculer u1
En divisant x² par -x + 20, calculer u2
3- On généralise la méthode initiée à la question 2 ; prouver que pour n >= à 0 on a :
x^(n+1) = (x^n)(x-20) + 20x^n .
En déduire que pour n>= 0 on a : un+1 = 20un - 1/(n+1)
Voilà , je suis bloqué pour cette partie, merci d'avance pour votre aide :we:
Yo
Intégration par parties
Kikoo <3 Bieber a écrit:Je ne pense pas que cela soit la bonne réponse :
Par IPP, on a :si j'ai pas fait d'erreurs.
En regardant la question 3, je pense que tu ne t'es pas trompé.. :we:
Mais je n'ai pas souvenir d'avoir fait les IPP avec les dx à l'intérieur en cours, donc je ne sais pas comment faire pour u2..
Peux-tu m'aider ?
Billball a écrit:
tu peux écrire x²/(-x+20)
comme -x²/(20-x) donc ensuite tu t'amuser à écrire A + B/(20-x) + C
avec A = ....x , B = ...x , C = ... (unités) ou en réduisant au même dénominateur, tu trouves x²
Je ne vois pas à quoi cela pourrait servir.. :hum:
Kikoo <3 Bieber a écrit:Pour, je sens la double IPP, mais ce n'est point judicieux vu ce que t'a proposé Billball.
@BB : Il suffit de s'y faire...
oui c'est sur ca marche avec double IPP, simplement si il a u5 à calculer t'as pas finis :ptdr:
donc bidouille un peu et si ya soucis et que tu trouves pas, ben on t'éclairera
Billball a écrit:oui c'est sur ca marche avec double IPP, simplement si il a u5 à calculer t'as pas finis :ptdr:
donc bidouille un peu et si ya soucis et que tu trouves pas, ben on t'éclairera
Je trouve vraiment pas, je crois pas avoir fait les doubles IPP en cours, ou alors très vite fait..
Je comprends vraiment pas ce DM, pourtant d'habitude j'y arrive à peu près et là je bloque au début :mur:
Alors, tu fais ton IPP...
On va dire que tu dois intégrer un truc du genre :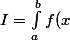\mathrm{d}x) avec
avec =u'(x)\cdot v(x))
Ca te fait :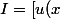v(x)\right]_a^b-\int_a^b u(x)v'(x)\mathrm{d}x)
Mais si intégrerv'(x)\mathrm{d}x) n'est pas trivial, il va falloir recommencer en se concentrant uniquement sur cette intégrale, en identifiant, et rebelote...
n'est pas trivial, il va falloir recommencer en se concentrant uniquement sur cette intégrale, en identifiant, et rebelote...
Et on continue ad libitum tant qu'on a pas eu un truc intégrable.
C'est sur que pour calculer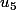 ... :mur: :mur: :mur:
... :mur: :mur: :mur:
On va dire que tu dois intégrer un truc du genre :
Ca te fait :
Mais si intégrer
Et on continue ad libitum tant qu'on a pas eu un truc intégrable.
C'est sur que pour calculer
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
