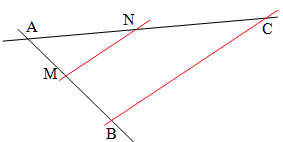
Les points A, M et B sont alignés dans cet ordre,
Les points A, N et C sont alignés dans cet ordre
De plus les droite (MN) et (BC) sont parallèles
Donc, d'après le théorème de Thalès, on a :
antonyme a écrit:Voici un exemple avec cette figure :
Les points A, M et B sont alignés dans cet ordre,
Les points A, N et C sont alignés dans cet ordre
De plus les droite (MN) et (BC) sont parallèles
Donc, d'après le théorème de Thalès, on a :
Illona a écrit:0ui ça je sais, mais ce que je ne comprends pas c'est comment le mettre sous forme d'équation ? :triste:
Illona a écrit:Donc sur ma copie je dois mettre ça : Les points B, G et A sont alignés dans cet ordre,
Les points B, F et C sont alignés dans cet ordre,
Et les droites (GF) et (AC) sont parallèles.
D'aorès le théorème de Thalés on a :
antonyme a écrit:C'est tout à fait vrai... Sauf que tu ne connais ni BF ni BG et ça ne permettra pas de trouver c
En revanche tu connais AD, AH, GD et BH donc il faut appliquer ce théorème dans le triangle ABH
Comme tu as compris la méthode je te le donne :
Les points A, M et B sont alignés dans cet ordre,
Les points A, N et C sont alignés dans cet ordre
De plus les droite (MN) et (BC) sont parallèles
Donc, d'après le théorème de Thalès, on a :
Ici c'est l'égalité qui nous intéresse, il faut remplacer par leur valeur ou leur expression en fonction de c :,
,
et
Puis on simplifie tous ça afin de trouver c :we:
Illona a écrit:Donc pour moi c'est légalité
antonyme a écrit:Ici c'est l'égalitéqui nous intéresse, il faut remplacer par leur valeur ou leur expression en fonction de c :
,
,
et
Puis on simplifie tous ça afin de trouver c :we:
antonyme a écrit:Non non, je te l'ai dit clairement : cette égalité est vraie (tout comme 1=1) mais elle ne sert à rien.
Tu as bien appliqué Thalès mais tu l'as fait au mauvaise endroit. Comme tu avais compris la méthode je l'ai fait pour toi au bonne endroit (c-à-d là où c'est utile).
Maintenant à toi de continuer avec ça :
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :