Integrale

[Mulan]

Bonjour, pouvez vous m'expliquer comment resoudre ces questions.

1) Montrer que integrale de t=0 à 1 de t^n f(t) = f(1)/n + o(1/n)
on suppose que f est continue sur [ 0,1 ]

2) Déterminer les f continues tel que pour tout x dans R,
f(x) + int de 0 à x de (x-t) f(t) dt = 1

3) Soit Ix = int de 0 à pi/2 de ln(cos²t +x² sin²t)dt
Mq I est C1
Calculer I'x et donner I(x)

Pour le 1) J'ai regarder si f(t) = 0 mais apres je ne vois pas comment mi prendre

Merci !

[girdav]

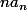
Pose et montre que tend vers .

[Mulan]

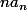
Pose et montre que tend vers .

Comment puis je montrer vu que je ne connais rien sur f ?

[girdav]

Si, tu sais qu'elle est continue, c'est suffisant ici.

[Mulan]

Si, tu sais qu'elle est continue, c'est suffisant ici.

je n'arrive pas à montrer la limite car n tend vers + infini ce qui me bloque pour trouver 0, car même si l'integrale tend vers 0 j 'ai une forme indeterminée

[girdav]

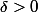
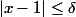
Il faut y aller à coup de : pour fixé, on peut trouver tel que si , alors . Puis regarde l'intégrale sur et .

[Mulan]

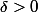
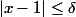
Il faut y aller à coup de : pour fixé, on peut trouver tel que si , alors . Puis regarde l'intégrale sur et .

D'accord, merci beaucoup

2) J'ai essayé de chercher à tatons mais je tombe sur aucune fonction f y a t il une méthode ?

Merci

[girdav]

Pour la deux, est dérivable; on peut chercher une équation différentielle satisfaite par .

[Mulan]

Pour la deux, est dérivable; on peut chercher une équation différentielle satisfaite par .

Euh je ne vois pas comment poser une equa diff ?

[girdav]

En dérivant des deux côtés de l'équation.

[Mulan]

En dérivant des deux côtés de l'équation.

Petite question pouvez vous m'expliqer comment deriver une integrale car a chaque fois j 'enleve juste l'integrale mais selon les bornes c'est faux

[girdav]

Ici, il faut développer , sortir le du premier membre puis utiliser le "théorème fondamental de l'analyse".