Problème de développement limité

[arnaud75]

Bonjour,

J'ai un probléme avec cet exercice :

c'est f(x)= (1+x)^(1/x)

Pour la question 2) : f(x)= exp((1/x)*ln(1+x))
Je fais donc un DL(2) de ln(1+x) puis de e(h) en posant h=(1/x)*ln(1+x) puis je compose les DL et je ne trouve pas la réponse et je ne comprends comment on obtient des "e" dans l'expression du DL
Pourriez vous me dire comment y parvenir ?!
Merci d'avance !

[ev85]

Bonjour,

J'ai un probléme avec cet exercice :

c'est f(x)= (1+x)^(1/x)

Pour la question 2) : f(x)= exp((1/x)*ln(1+x))
Je fais donc un DL(2) de ln(1+x) puis de e(h) en posant h=(1/x)*ln(1+x) puis je compose les DL et je ne trouve pas la réponse et je ne comprends comment on obtient des "e" dans l'expression du DL
Pourriez vous me dire comment y parvenir ?!
Merci d'avance !

[arnaud75]

Je ne vois pas où et quand le exp(1+h) intervient...

[ev85]

Je ne vois pas où et quand le exp(1+h) intervient...

donc
.
Tu le vois le ?

[arnaud75]

donc
.
Tu le vois le ?

J'ai trouvé le ça pour le DL de (ln(1+x)/x) mais je ne vois pas le h...
Pour moi h=(ln(1+x)/x) mais tu as peut être posé h= 1+(-x/2)+(x^2/3) non ?!

[ev85]

J'ai trouvé le ça pour le DL de (ln(1+x)/x) mais je ne vois pas le h...
Pour moi h=(ln(1+x)/x) mais tu as peut être posé h= 1+(-x/2)+(x^2/3) non ?!

Le problème, c'est que ton h tend vers 1, pas vers zéro.

[arnaud75]

Le problème, c'est que ton h tend vers 1, pas vers zéro.

Ah voilà c'était ça mon probléme ! Merci !

[arnaud75]

Je crois que j'ai toujours pas compris !

J'ai posé u= h-1 .
d'où exp(h)= exp(u+1)
j'ai réalisé un DL(2) en o de exp(u+1)
J'ai donc exp(u)*exp(1) quand u tend vers 0 =e +eu +(e(u^2)/2) + o(u^2)

Aprés je fais quoi je remplace u par (h-1) ? et je fais un DL de exp(h) quand h tend vers 1 ?

[cdav]

Bonjour,

J'ai un probléme avec cet exercice :

c'est f(x)= (1+x)^(1/x)

Pour la question 2) : f(x)= exp((1/x)*ln(1+x))
Je fais donc un DL(2) de ln(1+x) puis de e(h) en posant h=(1/x)*ln(1+x) puis je compose les DL et je ne trouve pas la réponse et je ne comprends comment on obtient des "e" dans l'expression du DL
Pourriez vous me dire comment y parvenir ?!
Merci d'avance !

ln(1+x)=x-x^2/+..
exp(1/x*ln(1°x)=exp(1-x/2+....)
tu mets e en facteur et tu utilises un DL de exp en 0

[cdav]

1

donc
.
Tu le vois le ?

f(x)=exp(1/x*ln(1+x))=exp(1/x*(x-x^2/2+x^3/3+o(x^3))
=exp(1-x/2+x^2/3+o(x^2))
=e*exp(-x/2+x^2/3+o(x^2))
=e*(1-x/2+x^2/3+x^2/4+o(x^2))

voila

http://www.ismath.fr

[ev85]

1



f(x)=exp(1/x*ln(1+x))=exp(1/x*(x-x^2/2+x^3/3+o(x^3))
=exp(1-x/2+x^2/3+o(x^2))
=e*exp(-x/2+x^2/3+o(x^2))
=e*(1-x/2+x^2/3+x^2/4+o(x^2))

voila

http://www.ismath.fr

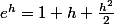
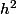
Euh... + des bananes. Il ne faut pas oublier de diviser le par deux !

[cdav]

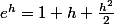
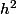
Euh... + des bananes. Il ne faut pas oublier de diviser le par deux !

certes tu as raison

[arnaud75]

Mais comment on trouve le (11e/24)x^2 ?!

[cdav]

Mais comment on trouve le (11e/24)x^2 ?!

f(x)=e*(1-x/2+x^3/3+x^2/8+o(x^2))
=e(1-x/2+11/24x^2+o(x^2))

[arnaud75]

oulalalala : je vais me poser et tout reprendre ! Merci à vous deux !

[cdav]

Mais comment on trouve le (11e/24)x^2 ?!

f(x)=e*(1-x/2+x^3/3+x^2/8+o(x^2))
=e(1-x/2+11/24x^2+o(x^2))

[fatal_error]

cdav,

ca va on compris pour ton lien. Tu le signales dans un et un seul poste, par exemple dans une discussion dans le café mathématique que tu crèes, mais il est inutile de l'écrire dans chacun de tes posts, ca se rapporte à du spam.

Merci de ta compréhension

[arnaud75]

C'est bon j'ai enfin et définitivement compris ! Merci à tous de votre précieuse aide !